Advertisements
Advertisements
प्रश्न
A rectangular tank 15m long and 11m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5m. Find least height of tank that will serve purpose .
उत्तर
Given length of rectangular tank = 15m
Breath of rectangular tank = 11m
Let height of rectangular tank be h
Volumeof rec tan gular tan k = lbh
Volume = 15 x 11 x h ____(1)
Given radius of cylindrical tank (r) =`21/2m`
Length/height of tank = 5m
Volume of cylindrical tan k = πr2h
`=pi(21/2)^2xx5` _______(2)
Since volumes are equal
Equating (1) and (2)
`15xx11xxh=pi(21/2)^2xx5`
⇒ `h=(22/7xx(21/2)^2xx5)/(15xx11)`
⇒ h = 10.5m
∴ Height of tank = 10.5m
APPEARS IN
संबंधित प्रश्न
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
A solid metallic sphere of radius 8 cm is melted and recast into spherical balls each of radius 2 cm. Find the number of spherical balls obtained.
A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone of base radius 8 cm. The height of the cone is
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
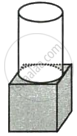
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
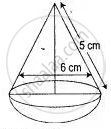
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m calculate the length of the canvas which is 5m wide to make the required tent.
The volume (in cm3) of the largest right circular cone that can be cut off from a cube of edge 4.2 cm is ______.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
