Advertisements
Advertisements
प्रश्न
A rocket with a lift-off mass 20,000 kg is blasted upwards with an initial acceleration of 5.0 m s–2. Calculate the initial thrust (force) of the blast.
उत्तर
Mass of the rocket, m = 20,000 kg
Initial acceleration, a = 5 m/s2
Acceleration due to gravity, g = 10 m/s2
Using Newton’s second law of motion, the net force (thrust) acting on the rocket is given by the relation:
F – mg = ma
F = m (g + a)
= 20000 × (10 + 5)
= 20000 × 15 = 3 × 105 N
APPEARS IN
संबंधित प्रश्न
Explain why a cricketer moves his hands backwards while holding a catch.
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
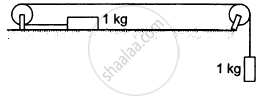
Calculate the tension in the string shown in the following figure. The pulley and the string are light and all the surfaces are frictionless. Take g = 10 m/s2.
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
The unit of linear momentum is :
Calculate the magnitude of force which when applied on a body of mass 0.5 kg produces an acceleration of 5 m s-2.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
State Newton's second law of motion.
A body of mass 400 g is resting on a frictionless table. Find the acceleration of the body when acted upon by a force of 0.02 N.
The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin 4 pt for 0 < t < (1/4) s (A > o), and x = 0 for t > (1/4) s. Which of the following statements is true?
- The force at t = (1/8) s on the particle is – 16π2 Am.
- The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
- The particle is not acted upon by any force.
- The particle is not acted upon by a constant force.
- There is no impulse acting on the particle.
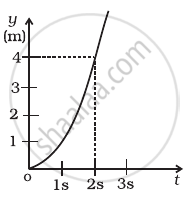
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.