Advertisements
Advertisements
प्रश्न
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
Let the radius of sphere = r
When a solid ball is exactly fitted inside the cubical box of side a,
We get,
Diameter of ball = Edge length of cube
2r = a
Radius, r = `"a"/2`
We also know that,
Volume of sphere = `4/(3π"r"^3)`
Volume of ball = `4/3π("a"/2)^3`
= `4/3π("a"^3/8)`
= `1/6π"a"^3`
APPEARS IN
संबंधित प्रश्न
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42cm and height 21cm which are filled completely. Find the diameter of cylindrical vessel?
The difference between outer and inner curved surface areas of a hollow right circular cylinder 14cm long is 88cm2. If the volume of metal used in making cylinder is 176cm3.find the outer and inner diameters of the cylinder____?
An iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is 1/4 of the radius of the original ball, how many such balls are made? Compare the surface area, of all the smaller balls combined together with that of the original ball.
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A cylindrical road roller made of iron is 1 m long, Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm3 of iron has 7.8 gm mass. (Use π = 3.14)
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
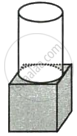
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
The largest sphere is carved out of a solid cube of side 21 cm. Find the volume of the sphere.
