Advertisements
Advertisements
प्रश्न
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.
उत्तर
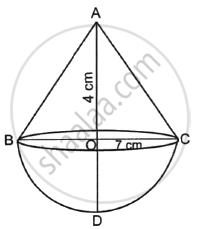
Volume of solid = `1/3πr^2h + 2/3πr^3`
= `1/3πr^2 (h + 2r)`
= `π/3 xx (7)^2 xx (4 + 2 xx 7)`
= `π/3 xx 49 xx 18`
= 294π cm3
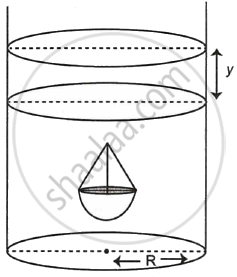
Let y be the height rise of water in a cylindrical cylinder with radius R = 14 cm.
∴ Volume of water rise in a cylindrical container = Volume of solid immersed
πR2y = 294π
`\implies` π(14)2y = 294π
∴ y = `294/(14 xx 14)`
= `21/14`
= `3/2`
= 1.5 cm
Hence, The rise in the water level is y = 1.5 cm
APPEARS IN
संबंधित प्रश्न
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
Choose the correct answer of the following question:
A metallic solid sphere of radius 9 cm is melted to form a solid cylinder of radius 9 cm. The height of the cylinder is
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
How many bags of grain can be stored in a cuboidal granary (8 m × 6 m × 3 m), if each bag occupies a space of 0.64 m3?
A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone of base radius 8 cm. The height of the cone is
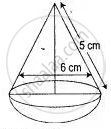
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
How many bags of grain can be stored in a cuboid granary 12 m × 6 m × 5 m. If each bag occupies a space of 0.48 m3?
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
