Advertisements
Advertisements
प्रश्न
A sphere can roll on a surface inclined at an angle θ if the friction coefficient is more than \[\frac{2}{7}g \tan\theta.\] Suppose the friction coefficient is \[\frac{1}{7}g\ tan\theta.\] If a sphere is released from rest on the incline, _____________ .
पर्याय
it will stay at rest
it will make pure translational motion
it will translate and rotate about the centre
the angular momentum of the sphere about its centre will remain constant
उत्तर
it will translate and rotate about the centre
The given coefficient of friction \[\left(\frac{1}{7}g\ tan\theta\right)\] is less than the coefficient friction \[\left(\frac{2}{7}g\ tan\theta\right)\] required for perfect rolling of the sphere on the inclined plane.
Therefore, sphere may slip while rolling and it will translate and rotate about the centre.
APPEARS IN
संबंधित प्रश्न
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Can an object be in pure translation as well as in pure rotation?
Two uniform solid spheres having unequal masses and unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping, ___________ .
A hollow sphere and a solid sphere having same mss and same radii are rolled down a rough inclined plane.
In rear-wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road the friction
(a) on the rear wheels is in the forward direction
(b) on the front wheels is in the backward direction
(c) on the rear wheels has larger magnitude than the friction on the front wheels
(d) on the car is in the backward direction.
A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
A solid sphere of mass 0⋅50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object rolls without slipping.
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along with a horizontal table with a velocity of 20 cms-1. (take the surface of the table as reference)
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
A man is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity `omega`. The tension in the strings is F. If the length of string and angular velocity are doubled, the tension in string is now ____________.
A solid sphere is rolling on a frictionless surface with translational velocity 'V'. It climbs the inclined plane from 'A' to 'B' and then moves away from Bon the smooth horizontal surface. The value of 'V' should be ______.
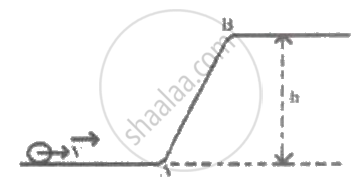
A solid spherical ball rolls on an inclined plane without slipping. The ratio of rotational energy and total energy is ______.
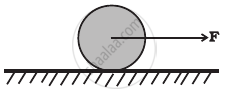
A uniform disc of radius R, is resting on a table on its rim.The coefficient of friction between disc and table is µ (Figure). Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?
Solid spherical ball is rolling on a frictionless horizontal plane surface about is axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is ______.
If x = at + bt2, where x is the distance travelled by the body in kilometers while t is the time in seconds, then the unit of b is ______.
The kinetic energy and angular momentum of a body rotating with constant angular velocity are E and L. What does `(2E)/L` represent?
