Advertisements
Advertisements
प्रश्न
A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure. (a) Show that the magnetic force acting on the part PQ is equal and opposite to the part RS. (b) Find the magnetic force on the square loop.
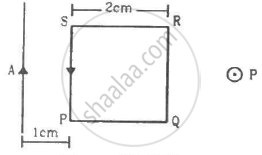
उत्तर
Given:
Current in the loop, i1 = 6 A
Current in the wire, i2 = 10 A
Now, consider an element on PQ of width dx at a distance x from the wire.
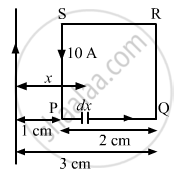
Force on the element is given by \[dF = \frac{\mu_0 i_1 i_2}{2\pi x}dx\]
Force acting on part PQ is given by
\[F_{PQ} = \frac{\mu_0 i_1 i_2}{2\pi} \int\limits_1^3 \frac{dx}{x}\]
\[ = 2 \times {10}^{- 7} \times 6 \times 10[\text{ ln } x {]_1}^3 \]
\[ = 120 \times {10}^{- 7} \text{ ln } \left( 3 \right) N\]
\[\text{ Similarly }, \]
\[ F_{RS} = \frac{\mu_0 i_1 i_2}{2\pi} \int\limits_3^1 \frac{dx}{x}\]
\[ = 120 \times {10}^{- 7} \text{ ln } \left( \frac{1}{3} \right)\]
\[ = - 120 \times {10}^{- 7} \text{ ln } \left( 3 \right) N\]
Both forces are equal in magnitude, but they are opposite in direction.
(b) The magnetic field intensity due to wire on SP is given by
\[F_{SP} = i_1 Bl\]
\[ = \frac{\mu_0 i_1 i_2}{2\pi}\left( \frac{l}{r} \right)\]
\[ = \frac{\mu_0 i_1 i_2}{2\pi}\left( \frac{2}{1} \right)\]
(Towards right)
Force on part RQ is given by
\[F_{RQ} = i_1 Bl\]
\[ = \frac{\mu_0 i_1 i_2}{2\pi}\left( \frac{l}{r} \right)\]
\[ = \frac{\mu_0 i_1 i_2}{2\pi}\left( \frac{2}{3} \right)\]
(Towards left)
Thus, the net force on the loop is given by
\[F_{net} = F_{SP} - F_{RQ} \]
\[ = \frac{\mu_0 i_1 i_2}{2\pi}\left( \frac{2}{1} - \frac{2}{3} \right)\]
\[ = 2 \times {10}^{- 7} \times 6 \times 10 \times \frac{4}{3}\]
\[ = 16 \times {10}^{- 6}\] N
(Towards right)
APPEARS IN
संबंधित प्रश्न
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnitude 0.20 T exists parallel to the longer side of the loop. (a) What is the force acting on the loop? (b) What is the torque acting on the loop?
A circular loop carrying a current i is made of a wire of length L. A uniform magnetic field B exists parallel to the plane of the loop. (a) Find the torque on the loop. (b) If the same length of the wire is used to form a square loop, what would be the torque? Which is larger?
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
A small cylindrical soft iron piece is kept in a galvanometer so that
A rectangular coil has 200 turns each of area 50 cm2 . It is capable of rotation about an axis joining the mid points of two opposite sides. When a current of 10 A is passed through it while its plane is at right angles to a uniform magnetic field, it experiences a torque of 5 Nm. The magnetic field will be ____________.
The sensitivity of a milliammeter of range 0 to 50 mA is x `"div"/"mA"`. If it is converted into an ammeter of range 500 mA by using a suitable shunt then the sensitivity will be ________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
If the net magnetic force acting on a loop is zero then ____________.
The current flowing through moving coil galvanometer is 20% of the current to be measured. The resistance of moving coil galvanometer is 48 `Omega`, then shunt required is ____________.
Which one of the following statements is 'NOT' TRUE? Sensitivity of a moving coil galvanometer can be increased by ____________.
The magnetic field developed due to current carrying coil at its centre is 'B'. If the new coil of two turns is prepared from the above coil and same current is passed, then the magnetic field at the centre of the new coil will be ____________.
An ammeter is obtained by shunting 'n' `Omega` galvanometer with 'n' `Omega` resistance. The additional shunt required to be connected across it to double the range is ____________.
A circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field `Bhati`. The torque on the coil due to the magnetic field is ______.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom, given the radius of the orbit is 2.1 Å and the orbital speed is 1.1 × 106 m/s.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
