Advertisements
Advertisements
प्रश्न
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects the co-ordinate axes at points A and B. M is the mid-point of the segment AB. Find:
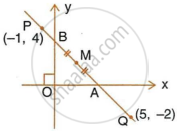
- The equation of the line.
- The co-ordinates of A and B.
- The co-ordinates of M.
उत्तर
i. Slope of PQ =`(-2 - 4)/(5 + 1) = (-6)/6 = -1`
Equation of the line PQ is given by
y – y1 = m(x – x1)
y − 4 = −1(x + 1)
y − 4 = −x − 1
x + y = 4 − 1
x + y = 3
ii. For point A (on x-axis), y = 0.
Putting y = 0 in the equation of PQ, we get,
x = 3
Thus, the co-ordinates of point A are (3, 0).
For point B (on y-axis), x = 0.
Putting x = 0 in the equation of PQ, we get,
y = 3
Thus, the co-ordinates of point B are (0, 3).
iii. M is the mid-point of AB.
So, the co-ordinates of point M are
`( (3 + 0)/2 , (0 + 3)/2) = (3/2, 3/2)`
APPEARS IN
संबंधित प्रश्न
In the given figure ABCD is a rectangle. It consists of a circle and two semi-circles each of
which are of radius 5 cm. Find the area of the shaded region. Give your answer correct to
three significant figures

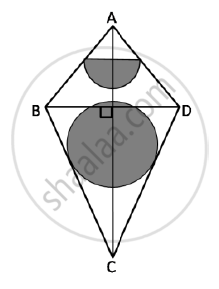
The given figure represents a kite with a circular and a semicircular motifs stuck on it.
The radius of a circle is 2.5 cm and the semicircle is 2 cm. If diagonals AC and BD are
of lengths 12 cm and 8 cm respectively, find the area of the:
1) Shaded part. Give your answer correct to the nearest whole number.
2) Unshaded part
Show that A(3, 2), B(6, −2) and C(2, −5) can be the vertices of a square.
- Find the co-ordinates of its fourth vertex D, if ABCD is a square.
- Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.
O(0, 0), A(3, 5) and B(−5, −3) are the vertices of triangle OAB. Find the equation of median of triangle OAB through vertex O.
O(0, 0), A(3, 5) and B(−5, −3) are the vertices of triangle OAB. Find the equation of altitude of triangle OAB through vertex B.
A line AB meets the x-axis at point A and y-axis at point B. The point P(−4, −2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:
- the co-ordinates of A and B.
- equation of line through P and perpendicular to AB.
Point A and B have co-ordinates (7, −3) and (1, 9) respectively. Find:
- the slope of AB.
- the equation of perpendicular bisector of the line segment AB.
- the value of ‘p’ of (−2, p) lies on it.
Use a graph sheet for this question.
Take 1 cm = 1 unit along both x and y axis.
(i) Plot the following points:
A(0,5), B(3,0), C(1,0) and D(1,–5)
(ii) Reflect the points B, C and D on the y axis and name them as B',C'andD' respectively.
(iii) Write down the coordinates of B',C 'and D'
(iv) Join the point A, B, C, D, D ', C ', B', A in order and give a name to the closed figure ABCDD'C'B
A line is of length 10 units and one end is at the point (2, – 3). If the abscissa of the other end be 10, prove that its ordinate must be 3 or – 9.
Use a graph sheet for this question, take 2 cm = 1 unit along both x and y-axis:
- Plot the points A (3, 2) and B (5, 0). Reflect point A on the y-axis to A΄. Write co-ordinates of A΄.
- Reflect point B on the line AA΄ to B΄. Write the co-ordinates of B΄.
- Name the closed figure A’B’AB.
