Advertisements
Advertisements
प्रश्न
A student wants to project the image of a candle flame on a screen 80 cm in front of a mirror by keeping the candle flame at a distance of 20 cm from its pole.
- Which type of mirror should the student use?
- Find the magnification of the image produced.
- Find the distance between the object and its image.
- Draw a ray diagram to show the image formation in this case and mark the distance between the object and its image.
उत्तर
(a) A real image can be projected on a screen using a concave mirror. In the given case, the student should use a concave mirror.
(b) \[\text{ Magnification }\left( m \right)\text{ is given by }\]
\[m = - \frac{v}{u}\]
Here,
\[u = \text{ Distance of the object }\]
\[v =\text{ Distance of the image }\]
\[ \therefore m = \frac{- \left( - 80 \right)}{\left( - 20 \right)} = - 4\]
(c)
The object and the image are on the same side of the mirror.
Distance of the object from the lens = 20 cm
Distance of the image from the lens = 80 cm
Thus,
Distance between the object and the image = 80 − 20 = 60 cm
(d)
To draw a ray diagram, we need to find the focal length of the mirror.
According to the mirror formula,
\[\frac{1}{f} = \frac{1}{u} + \frac{1}{v}\]
Here,
u = Distance of the object
v = Distance of the image
f = Focal length of the mirror
Now,
\[\frac{1}{f} = \frac{1}{- 20} + \frac{1}{- 80}\]
\[ \Rightarrow \frac{1}{f} = - \left( \frac{4 + 1}{80} \right)\]
\[ \Rightarrow \frac{1}{f} = - \left( \frac{5}{80} \right)\]
\[ \Rightarrow f = - \left( \frac{80}{5} \right) = - 16 cm\]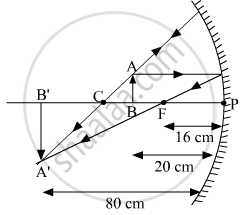
APPEARS IN
संबंधित प्रश्न
A student is using a convex lens of focal length 10 cm to study the image formation by a convex lens for the various positions of the object. In one of his observations, he may observe that when the object is placed at a distance of 20 cm from the lens, its image is formed at (select the correct option)
(A) 20 cm on the other side of the lens and is of the same size, real and erect.
(B) 40 cm on the other side of the lens and is magnified, real and inverted.
(C) 20 cm on the other side of the lens and is of the same size, real and inverted.
(D) 20 cm on the other side of the lens and is of the same size, virtual and erect.
An object of height 4 cm is placed at a distance of 20 cm from a concave lens of focal length 10 cm. Use lens formula to determine the position of the image formed.
The image of a candle flame placed at a distance of 30 cm from a spherical lens is formed on a screen placed on the other side of the lens at a distance of 60 cm from the optical centre of the lens. Identify the type of lens and calculate its focal length. If the height of the flame is 3 cm, find the height of its image.
A student has obtained an image of a distant object on a screen to determine the focal length F1 of the given lens. His teacher, after checking the image, gave him another lens of focal length F2 and asked him to focus the same object on the same screen. The student found that to obtain a sharp image, he has to move the lens away from the screen. From this finding, we may conclude that both the lenses given to the student were :
(A) Concave and F1 < F2
(B) Convex and F1 < F2
(C) Convex and F1 > F2
(D) Concave and F1 > F2
What is the difference between a real image and a virtual image? Give one example of each type of image
Draw a diagram to show how a converging lens held close to the eye acts as a magnifying glass. Why is it usual to choose a lens of short focal length for this purpose rather than one of long focal length?
Explain what is meant by a virtual, magnified image.
Draw a ray diagram to show the formation of a virtual magnified image of an object by a convex lens. In your diagram, the position of object and image with respect to the principal focus should be shown clearly.
An object is placed at a distance of 20 cm in front of a concave lens of focal length 20 cm.
- Find the position of the image, and
- the magnification of the image.
Magnification of a convex lens is
