Advertisements
Advertisements
प्रश्न
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2.
(Note that the base of the tent will not be covered with canvas.) [Use `pi = 22/7`]
उत्तर

Given that,
Height (h) of the cylindrical part = 2.1 m
Diameter of the cylindrical part = 4 m
Radius of the cylindrical part = 2 m
Slant height (l) of conical part = 2.8 m
Area of canvas used = CSA of conical part + CSA of cylindrical part
πrl + 2πrh
= `π xx 2 xx 2.8+2π xx 2 xx2.1`
= `2π[2.8+2 xx 2.1]`
= `2π[2.8 + 4.2]`
= `2 xx 22/7 xx 7`
= 44 m2
Cost of 1 m2 canvas = Rs 500
Cost of 44 m2 canvas = 44 × 500 = 22000
Therefore, it will cost Rs 22000 for making such a tent.
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
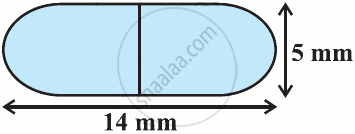
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
Radii of circular ends of a solid frustum off a cone re 33cm and 27cm and its slant height are 10cm. find its total surface area?
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459 `3/7` cm3. The radii of its lower and upper circular ends are 8cm and 20cm. find the cost of metal sheet used in making container at rate of Rs 1.4 per cm2?
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
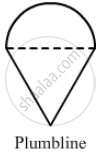
A plumbline (sahul) is a combination of
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
The shape of a gilli, in the gilli-danda game (see figure), is a combination of ______.
The total surface area of a solid hemisphere of radius 7 cm is ______.
