Advertisements
Advertisements
प्रश्न
A trapezium with 3 equal sides and one side double the equal side can be divided into ______ equilateral triangles of ______ area.
उत्तर
A trapezium with 3 equal sides and one side double the equal side can be divided into 3 equilateral triangles of equal area.
Explanation:
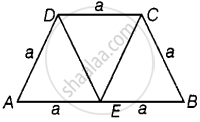
Let ABCD be a trapezium, in which
AD = DC = BC = a ...(say)
And AB = 2a ...[Given]
Draw medians through the vertices D and C on the side AB.
∴ AE = EB = a
Now, in parallelogram ADCE, we have
AD = EC = a and AE = CD = a ...[Opposite side in a parallelogram are equal]
In ΔADE and ΔDEC,
AD = EC
AE = CD
And DE = DE ...[Common]
BY SSS, ΔADE = ΔDEC
By triangle rule, ΔADE ≅ ΔDEC
Thus, ΔADE and ΔDEC are equilateral triangles having equal sides.
Similarly, in parallelogram DEBC, we can show that ΔDEC ≅ ΔECB.
Hence, the trapezium can be divided into 3 equilateral triangles of equal area.
APPEARS IN
संबंधित प्रश्न
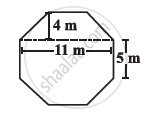
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 12 dm and 20 dm, altitude = 10 dm
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 150 cm and 30 dm, altitude = 9 dm.
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Find the area enclosed by each of the following figures [Fig. 20.49 (i)-(iii)] as the sum of the areas of a rectangle and a trapezium: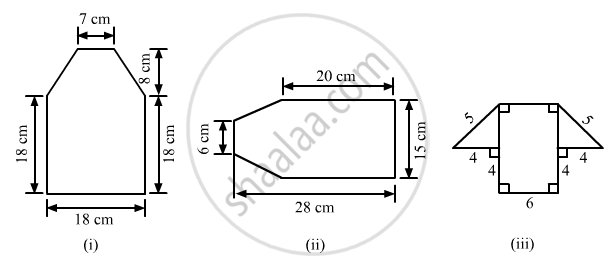
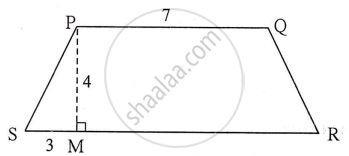
☐ PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of ☐ PQRS.
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
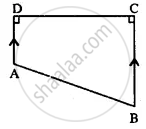
If the width DC, of the swimming pool, is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of the cross-section.
The parallel sides of a trapezium are in ratio 3: 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2; find the lengths of its parallel sides.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 10 m | 12 m | 20 m |
