Advertisements
Advertisements
प्रश्न
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number.
उत्तर
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is `10y + x`.
The product of the two digits of the number is 20. Thus, we have ` xy =20`
After interchanging the digits, the number becomes `10x + y`.
If 9 is added to the number, the digits interchange their places. Thus, we have
`(10y+x)+9=10x+y`
`⇒ 10y +x +9 =10x +y`
` ⇒ 1=x + y -10y -x =9`
` ⇒ 9x -9y =9`
`⇒ 9( x - y)=9`
` ⇒ x -y 9/9`
` ⇒ x - y =1`
So, we have the systems of equations
`xy=20`
`x-y=1`
Here x and y are unknowns. We have to solve the above systems of equations for xand y.
Substituting `x =1+y` from the second equation to the first equation, we get
`(1+y )y=20`
`⇒ y + y^2 = 20`
`⇒ y^2 + y = 20 =0`
` ⇒ y^2 + 5y -4y -20 =0`
`⇒ y (y + 5)-4(4+5)=0`
`⇒ ( y + 5)(y - 4)=0`
`⇒ y = -5` Or `y = 4`
Substituting the value of y in the second equation, we have

Hence, the number is `10 xx4 + 5= 45`.
Note that in the first pair of solution the values of x and y are both negative. But, the digits of the number can’t be negative. So, we must remove this pair.
APPEARS IN
संबंधित प्रश्न
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`5/(x-1) + 1/y-2 = 2`
`6/(x-1) - 3/(y-2) = 1`
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
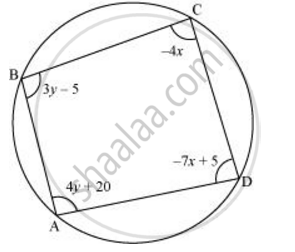
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
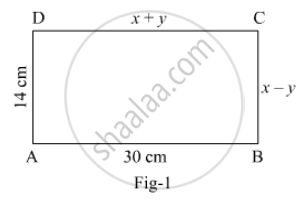
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs 2000. But if he sells the T.V. at 10% gain the fridge at 5% loss. He gains Rs 1500 on the transaction. Find the actual prices of T.V. and fridge.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages.
State with reason whether the point (3, −2) will lie on the graph of the equation 5m – 3n = − 21
