Advertisements
Advertisements
प्रश्न
आधार व्यास 2 cm और ऊँचाई 16 cm वाले धातु के एक ठोस बेलन को पिघला कर समान माप के बारह ठोस गोले बनाये जाते हैं। प्रत्येक गोले का व्यास ______ है।
पर्याय
4 cm
3 cm
2 cm
6 cm
उत्तर
आधार व्यास 2 cm और ऊँचाई 16 cm वाले धातु के एक ठोस बेलन को पिघला कर समान माप के बारह ठोस गोले बनाये जाते हैं। प्रत्येक गोले का व्यास 2 cm है।
स्पष्टीकरण:
जैसा कि हम जानते हैं,
बेलन का आयतन = πr2h
जहाँ r = आधार त्रिज्या,
h = सिलेंडर की ऊंचाई
दिए गए ठोस बेलन के लिए,
आधार व्यास = 2 cm
आधार त्रिज्या, r = 1 cm ...[त्रिज्या के रूप में = `1/2` व्यास]
ऊँचाई, h = 16 cm
बेलन का आयतन, V = π(1)2(16) = 16π cm3
अब,
माना गोले की त्रिज्या r है।
गोले का आयतन = `4/2 pi"r"^3`
जहाँ r = त्रिज्या
त्रिज्या r के 12 गोलों का आयतन = `12(4/3 pir^3) = 16 pir^3`
अब,
12 गोलों का आयतन = बेलन का आयतन ...[चूंकि आयतन समान रहता है, जब एक धातु की वस्तु को पिघलाकर दूसरी धातु की वस्तु में ढाला जाता है।]
⇒ 16πr3 = 16π
⇒ r3 = 1
⇒ r = `root(3)1` = 1 cm
व्यास = 2r = 2 cm
अतः, प्रत्येक गोले का व्यास 4 cm है।
APPEARS IN
संबंधित प्रश्न
एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्यूमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया है जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 सेमी है और इसकी लंबाई 12 सेमी है। यदि प्रत्येक शंकु की ऊँचाई 2 सेमी हो तो रचेल द्वारा बनाए गए मॉडल में अंतर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती है, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
एक सुराही निम्नलिखित का संयोजन ______ है।
दवाई का एक कैप्सूल 0.5 cm व्यास वाले एक बेलन के आकार का है, जिसके दोनों सिरों पर दो अर्धगोले लगे हुए हैं। संपूर्ण कैप्सूल की लंबाई 2 cm है। इस कैप्सूल की धारिता ______ है।
एक 3 cm, 4 cm और 5 cm किनारों वाले धातु के तीन ठोस घनों को पिघलाकर एक अकेला घन बनाया गया है। इस प्रकार बने घन का किनारा ज्ञात कीजिए।
विमाओं 9 cm × 11 cm × 12 cm वाले एक सीसे के घनाभाकार ठोस से 3 cm व्यास वाली कितनी गोलियाँ बनायी जा सकती हैं?
त्रिज्या 8 cm और ऊँचाई 12 cm वाले एक शंकु को उसकी अक्ष के मध्य-बिंदु से होकर जाने वाले और आधार के समांतर तल द्वारा दो भागों में विभाजित किया जाता है। दोनों भागों के आयतनों का अनपात ज्ञात कीजिए।
भुजा 7 cm वाले एक ठोस घन में 7 cm ऊंचाई और 3 cm त्रिज्या वाले एक शंकु के आकार का छेद् किया गया है। शेष ठोस का आयतन ज्ञात कीजिए।
दो ठोस शंकुओं को एक बेलनाकार नली में आकृति में दर्शाए अनुसार रखा जाता है। इनकी धारिताओं का अनुपात 2:1 है। इन शंकुओं की ऊँचाइयाँ और धारिताएँ ज्ञात कीजिए। बेलन के शेष भाग का आयतन भी ज्ञात कीजिए।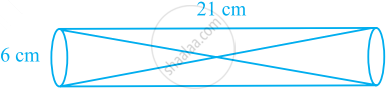
एक 7 cm व्यास वाले बेलनाकार बीकर, जिसमें कुछ पानी भरा है, में 1.4 cm व्यास वाले कंचे डाले जाते हैं। कंचों की वह संख्या ज्ञात कीजिए जिनको बीकर में डालने से पानी का स्तर 5.6 cm ऊपर उठ जायेगा।
