Advertisements
Advertisements
प्रश्न
त्रिज्या 8 cm और ऊँचाई 12 cm वाले एक शंकु को उसकी अक्ष के मध्य-बिंदु से होकर जाने वाले और आधार के समांतर तल द्वारा दो भागों में विभाजित किया जाता है। दोनों भागों के आयतनों का अनपात ज्ञात कीजिए।
उत्तर
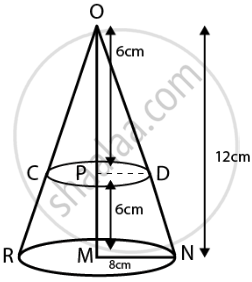
प्रश्न के अनुसार,
शंकु की ऊँचाई = OM = 12 cm
शंकु को मध्य-बिंदु से विभाजित किया गया है।
अत:, माना शंकु का मध्य-बिंदु = P
OP = PM = 6 cm
ΔOPD और ΔOMN से,
∠POD = ∠POD ...[सामान्य]
∠OPD = ∠OMN ...[दोनों 90°]
इसलिए, कोण-कोण समानता मानदंड द्वारा,
हमारे पास है,
ΔOPD ~ ΔOMN
और
समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं,
तो, हमारे पास हैं,
`"PD"/"MN" = "OP"/"OM"`
`"PD"/8 = 6/12`
PD = 4cm ...[MN = 8 cm = शंकु के आधार की त्रिज्या]
पहले भाग यानी शंकु के लिए
आधार त्रिज्या, r = PD = 4 cm
ऊँचाई, h = OP = 6 cm
हम जानते हैं कि,
त्रिज्या r और ऊंचाई h, V = `1/3 π"r"^2"h"` के लिए शंकु का आयतन,
पहले भाग का आयतन = `1/3 π(4)^(2)6` = 32π
दूसरे भाग के लिए, अर्थात फ्रस्टम
निचली त्रिज्या, r1 = MN = 8 cm
ऊपरी त्रिज्या, r2 = PD = 4 cm
ऊंचाई, h = PM = 6 cm
हम जानते हैं कि,
शंकु के छिन्नक का आयतन = `1/3 π"h"("r"_1^2 + "r"_2^2 + "r"_1"r"_2)`, जहाँ, h = ऊँचाई, r1 और r2 त्रिज्याएँ हैं, (r1 > r2)
दूसरे भाग का आयतन = `1/3 π(6)[8^2 + 4^2 + 8(4)]`
= 2π(112)
= 224π
इसलिए, हमें अनुपात मिलता है,
पहले भाग का आयतन : दूसरे भाग का आयतन = 32π : 224π = 1 : 7
APPEARS IN
संबंधित प्रश्न
एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 सेमी है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [प्रयोग करें π = `22/7`]
भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग π = `22/7`]
एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्यूमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया है जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 सेमी है और इसकी लंबाई 12 सेमी है। यदि प्रत्येक शंकु की ऊँचाई 2 सेमी हो तो रचेल द्वारा बनाए गए मॉडल में अंतर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढ़े बने हुए हैं। घनाभ की विमाएँ 15 सेमी 10 सेमी 3.5 सेमी हैं। प्रत्येक गड्ढ़े की त्रिज्या 0.5 सेमी है और गहराई 1.4 सेमी है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए। [π = `22/7`] का प्रयोग करें।
आधार व्यास 2 cm और ऊँचाई 16 cm वाले धातु के एक ठोस बेलन को पिघला कर समान माप के बारह ठोस गोले बनाये जाते हैं। प्रत्येक गोले का व्यास ______ है।
विमाओं 9 cm × 11 cm × 12 cm वाले एक सीसे के घनाभाकार ठोस से 3 cm व्यास वाली कितनी गोलियाँ बनायी जा सकती हैं?
दो ठोस शंकुओं को एक बेलनाकार नली में आकृति में दर्शाए अनुसार रखा जाता है। इनकी धारिताओं का अनुपात 2:1 है। इन शंकुओं की ऊँचाइयाँ और धारिताएँ ज्ञात कीजिए। बेलन के शेष भाग का आयतन भी ज्ञात कीजिए।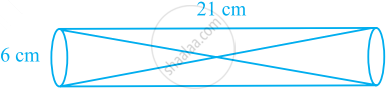
आधार 11 m × 6 m वाले एक घनाभाकार पानी की टंकी में 5 m की ऊँचाई तक पानी भरा है। यदि इस पानी को 3.5 m त्रिज्या वाली एक बेलनाकार टंकी में स्थानांतरित कर दिया जाये, तो इस बेलनाकार टंकी में पानी के स्तर की ऊँचाई ज्ञात कीजिए।
किसी फाउन्टेन पेन की नली, जो बेलन के आकार की है, 7 cm लंबी है और इसका व्यास 5 mm है। इस पेन की नली में पूरी भरी स्याही से औसतन 3300 शब्द लिखे जा सकते हैं। स्याही की उस बोतल से कितने शब्द लिखे जा सकते हैं, जिसमें 1 लीटर की `(1)/(5)` भाग स्याही है?
चावलों की एक ढेरी 9 m व्यास और 3.5 m ऊँचाई वाले एक शंकु के आकार की है। इन चावलों का आयतन ज्ञात कीजिए। इस ढेरी को केवल ढकने मात्र के लिए कितने कैनवस कपड़े की आवश्यकता होगी ?
