Advertisements
Advertisements
Question
त्रिज्या 8 cm और ऊँचाई 12 cm वाले एक शंकु को उसकी अक्ष के मध्य-बिंदु से होकर जाने वाले और आधार के समांतर तल द्वारा दो भागों में विभाजित किया जाता है। दोनों भागों के आयतनों का अनपात ज्ञात कीजिए।
Solution
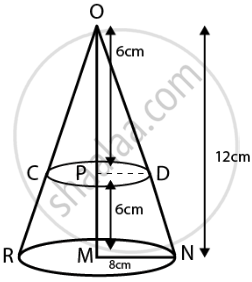
प्रश्न के अनुसार,
शंकु की ऊँचाई = OM = 12 cm
शंकु को मध्य-बिंदु से विभाजित किया गया है।
अत:, माना शंकु का मध्य-बिंदु = P
OP = PM = 6 cm
ΔOPD और ΔOMN से,
∠POD = ∠POD ...[सामान्य]
∠OPD = ∠OMN ...[दोनों 90°]
इसलिए, कोण-कोण समानता मानदंड द्वारा,
हमारे पास है,
ΔOPD ~ ΔOMN
और
समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं,
तो, हमारे पास हैं,
`"PD"/"MN" = "OP"/"OM"`
`"PD"/8 = 6/12`
PD = 4cm ...[MN = 8 cm = शंकु के आधार की त्रिज्या]
पहले भाग यानी शंकु के लिए
आधार त्रिज्या, r = PD = 4 cm
ऊँचाई, h = OP = 6 cm
हम जानते हैं कि,
त्रिज्या r और ऊंचाई h, V = `1/3 π"r"^2"h"` के लिए शंकु का आयतन,
पहले भाग का आयतन = `1/3 π(4)^(2)6` = 32π
दूसरे भाग के लिए, अर्थात फ्रस्टम
निचली त्रिज्या, r1 = MN = 8 cm
ऊपरी त्रिज्या, r2 = PD = 4 cm
ऊंचाई, h = PM = 6 cm
हम जानते हैं कि,
शंकु के छिन्नक का आयतन = `1/3 π"h"("r"_1^2 + "r"_2^2 + "r"_1"r"_2)`, जहाँ, h = ऊँचाई, r1 और r2 त्रिज्याएँ हैं, (r1 > r2)
दूसरे भाग का आयतन = `1/3 π(6)[8^2 + 4^2 + 8(4)]`
= 2π(112)
= 224π
इसलिए, हमें अनुपात मिलता है,
पहले भाग का आयतन : दूसरे भाग का आयतन = 32π : 224π = 1 : 7
APPEARS IN
RELATED QUESTIONS
एक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 सेमी है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [प्रयोग करें π = `22/7`]
भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग π = `22/7`]
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लंबाई 5 सेमी और व्यास 2.8 सेमी है।
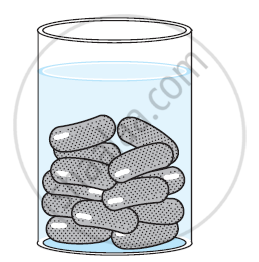
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढ़े बने हुए हैं। घनाभ की विमाएँ 15 सेमी 10 सेमी 3.5 सेमी हैं। प्रत्येक गड्ढ़े की त्रिज्या 0.5 सेमी है और गहराई 1.4 सेमी है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए। [π = `22/7`] का प्रयोग करें।
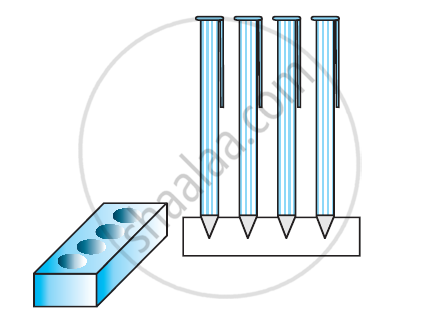
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती है, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
एक सुराही निम्नलिखित का संयोजन ______ है।
कोई मिस्री ईंटों से विमाओं 270 cm × 300 cm × 350 cm की एक दीवार बनाता है, जिनमें से प्रत्येक ईंट की माप 22.5 cm × 11.25 cm × 8.75 cm है। यदि यह मान लिया जाए कि दीवार का `1/8` भाग मसाले से भरा जाता है, तो दीवार को बनाने में लगी ईटों की संख्या ______ है।
आधार व्यास 2 cm और ऊँचाई 16 cm वाले धातु के एक ठोस बेलन को पिघला कर समान माप के बारह ठोस गोले बनाये जाते हैं। प्रत्येक गोले का व्यास ______ है।
भुजा a वाले एक घनाकार बक्से के अंदर एक ठोस गेंद पूर्णतया ठीक-ठीक रखी जा सकती है। गेंद का आयतन `4/3πa^3` है।
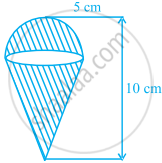
आकृति में, एक आइसक्रीम शंकु दर्शाया गया है, जिसमें आइसक्रीम भरी हुई है, तथा इसकी त्रिज्या 5 cm और ऊँचाई 10 cm है। आइसक्रीम का आयतन ज्ञात कीजिए, जबकि शंकु का `1/6` भाग आइसक्रीम से रिक्त रहता है।