Advertisements
Advertisements
Question
दो सर्वसम घनों, जिनमें से प्रत्येक का आयतन 64cm3 है, को सिरे से सिरा मिला कर जोड़ा जाता है। इस प्रकार प्राप्त घनाभ का पृष्ठीय क्षेत्रफल क्या है?
Solution
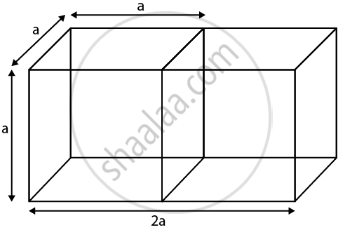
माना एक घन की भुजा = a
परिणामी घनाभ का पृष्ठीय क्षेत्रफल = 2(घन का कुल पृष्ठीय क्षेत्रफल) – 2(एकल पृष्ठ का क्षेत्रफल)
हम जानते हैं कि,
घन का कुल पृष्ठीय क्षेत्रफल = 6a2, जहाँ a = घन की भुजा
⇒ परिणामी घनाभ का पृष्ठीय क्षेत्रफल = 2(6a2) – 2(a2) = 10a2
भी,
प्रश्न के अनुसार,
घन का आयतन = 64 cm3
घन का आयतन = a3
64 = a3
a = 4 cm
इसलिए, परिणामी घनाभ का पृष्ठीय क्षेत्रफल = 10a2 = 10(4)2 = 160 cm2
APPEARS IN
RELATED QUESTIONS
दवा का एक कैप्सूल एक बेलन के आकार का है जिसके दोनों सिरों पर एक - एक अर्धगोला लगा हुआ है। पूरे कैप्सूल की लंबाई 14 मिमी है और उसका व्यास 5 मिमी है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग `pi = 22/7`]

कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 मी और 4 मी है तथा शंकु की तिर्यक ऊँचाई 2.8 मी है तो इस तंबू को बनाने में प्रयुक्त कैनवस का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500 रु प्रति वर्ग मी2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दें कि तम्बू का आधार कैनवास से ढका नहीं होगा।)
[उपयोग π = `22/7`]
एक साहुल निम्नलिखित का संयोजन है:
गिल्ली-डंडे के खेल में, गिल्ली का आकार निम्नलिखित का संयोजन है-

एक ही आधार त्रिज्या r वाले दो ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। तब नये ठोस का वक्र पृष्ठीय क्षेत्रफल ______ है।
समान आधार त्रिज्या r वाले दो सर्वसम ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। इस संयोजन का कुल पृष्ठीय क्षेत्रफल 6πr2 है।
त्रिज्या r और ऊचाई h वाले एक बेलन को उसी ऊँचाई और त्रिज्या वाले बेलन के ऊपर रख दिया जाता है। इस प्रकार बने आकार का कुल पृष्ठीय क्षेत्रफल 4πrh + 4πr2 है।
त्रिज्या r और ऊँचाई h वाले एक ठोस शंकु को उसी आधार त्रिज्या और ऊँचाई वाले एक ठोस बेलन के ऊपर रखा जाता है, जो शंकु की हैं। संयोजित ठोस का कुल पृष्ठीय क्षेत्रफल `pir[sqrt(r^2 + h^2) + 3r + 2h]` है।
एक बेलनाकार बर्तन, जिसकी तली में अर्धगोलाकार भाग आकृति में दर्शाए अनुसार ऊपर की ओर उठा हुआ है, की धारिता `(πr^2)/3[3h - 2r]` है।
समान आधार त्रिज्या 8 cm और समान ऊँचाई 15 cm वाले दो शंकुओं को उनके आधारों के अनुदिश जोड़ा जाता है। इस प्रकार बने आकार का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
