Advertisements
Advertisements
Question
समान आधार त्रिज्या r वाले दो सर्वसम ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। इस संयोजन का कुल पृष्ठीय क्षेत्रफल 6πr2 है।
Options
सत्य
असत्य
Solution
यह कथन असत्य है।
स्पष्टीकरण:
अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr2
यहां, समान त्रिज्या के दो समान ठोस गोलार्ध एक साथ चिपके हुए हैं।
अतः, दोनों गोलार्द्धों का आधार उभयनिष्ठ है।
∴ संयोजन का कुल पृष्ठीय क्षेत्रफल
= 2πr2 + 2πr2
= 4πr2
APPEARS IN
RELATED QUESTIONS
दवा का एक कैप्सूल एक बेलन के आकार का है जिसके दोनों सिरों पर एक - एक अर्धगोला लगा हुआ है। पूरे कैप्सूल की लंबाई 14 मिमी है और उसका व्यास 5 मिमी है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग `pi = 22/7`]

कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 मी और 4 मी है तथा शंकु की तिर्यक ऊँचाई 2.8 मी है तो इस तंबू को बनाने में प्रयुक्त कैनवस का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500 रु प्रति वर्ग मी2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दें कि तम्बू का आधार कैनवास से ढका नहीं होगा।)
[उपयोग π = `22/7`]
ऊँचाई 2.4 सेमी और व्यास 1.4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है। शेष बचे ठोस का निकटम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
[उपयोग π = `22/7`]
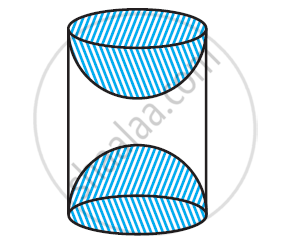
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा की आकृति में दिखाया गया है। यदि बेलन की ऊँचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग π = `22/7`]
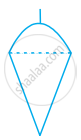
एक साहुल निम्नलिखित का संयोजन है:
विमाओं 49 cm × 33 cm × 24 cm के घनाभ के आकार के लोहे के किसी ठोस टुकड़े को पिघलाकर एक ठोस गोले के रूप में ढाला जाता है। गोले की त्रिज्या ______ है।
एक ही आधार त्रिज्या r वाले दो ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। तब नये ठोस का वक्र पृष्ठीय क्षेत्रफल ______ है।
त्रिज्या r और ऊचाई h वाले एक बेलन को उसी ऊँचाई और त्रिज्या वाले बेलन के ऊपर रख दिया जाता है। इस प्रकार बने आकार का कुल पृष्ठीय क्षेत्रफल 4πrh + 4πr2 है।
त्रिज्या r और ऊँचाई h वाले एक ठोस शंकु को उसी आधार त्रिज्या और ऊँचाई वाले एक ठोस बेलन के ऊपर रखा जाता है, जो शंकु की हैं। संयोजित ठोस का कुल पृष्ठीय क्षेत्रफल `pir[sqrt(r^2 + h^2) + 3r + 2h]` है।
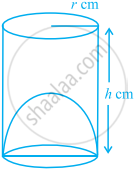
एक बेलनाकार बर्तन, जिसकी तली में अर्धगोलाकार भाग आकृति में दर्शाए अनुसार ऊपर की ओर उठा हुआ है, की धारिता `(πr^2)/3[3h - 2r]` है।