Advertisements
Advertisements
Question
ऊँचाई 2.4 सेमी और व्यास 1.4 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है। शेष बचे ठोस का निकटम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
[उपयोग π = `22/7`]
Solution
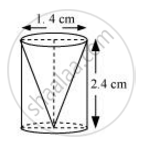
मान लीजिये,
शंक्वाकार भाग की ऊँचाई (h) = बेलनाकार भाग की ऊँचाई (h) = 2.4 cm
बेलनाकार भाग का व्यास = 1.4 सेमी
अत: बेलनाकार भाग की त्रिज्या (r) = 0.7 cm
शंक्वाकार भाग की तिरछी ऊँचाई (l) = `sqrt(r^2+h^2)`
`= sqrt((0.7)^2+(2.4)^2) `
`=sqrt(0.49+5.76)`
`=sqrt(6.25)`
= 2.5
शेष ठोस का कुल पृष्ठीय क्षेत्रफल होगा = बेलनाकार भाग का CSA + शंक्वाकार भाग का CSA + बेलनाकार आधार का क्षेत्रफल
= 2πrh + πrl + πr2
`= 2 xx 22/7 xx 0.7 xx 2.4+22/7 xx 0.7 xx 2.5+22/7 xx 0.7 xx 0.7`
= `4.4 xx 2.4 + 2.2 xx 2.5 + 2.2 xx 0.7`
= 10.56 + 5.50 + 1.54
= 17.60 cm2
शेष ठोस का निकटतम सेमी2 का कुल पृष्ठीय क्षेत्रफल 18 सेमी2 है।
APPEARS IN
RELATED QUESTIONS
कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 मी और 4 मी है तथा शंकु की तिर्यक ऊँचाई 2.8 मी है तो इस तंबू को बनाने में प्रयुक्त कैनवस का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500 रु प्रति वर्ग मी2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दें कि तम्बू का आधार कैनवास से ढका नहीं होगा।)
[उपयोग π = `22/7`]
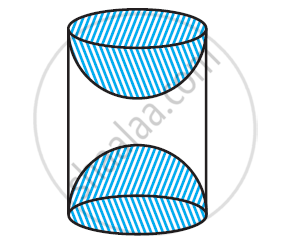
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा की आकृति में दिखाया गया है। यदि बेलन की ऊँचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग π = `22/7`]
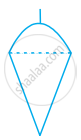
एक साहुल निम्नलिखित का संयोजन है:
विमाओं 49 cm × 33 cm × 24 cm के घनाभ के आकार के लोहे के किसी ठोस टुकड़े को पिघलाकर एक ठोस गोले के रूप में ढाला जाता है। गोले की त्रिज्या ______ है।
एक ही आधार त्रिज्या r वाले दो ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। तब नये ठोस का वक्र पृष्ठीय क्षेत्रफल ______ है।
समान आधार त्रिज्या r वाले दो सर्वसम ठोस अर्धगोलों को उनके आधारों के अनुदिश जोड़ दिया गया है। इस संयोजन का कुल पृष्ठीय क्षेत्रफल 6πr2 है।
त्रिज्या r और ऊँचाई h वाले एक ठोस शंकु को उसी आधार त्रिज्या और ऊँचाई वाले एक ठोस बेलन के ऊपर रखा जाता है, जो शंकु की हैं। संयोजित ठोस का कुल पृष्ठीय क्षेत्रफल `pir[sqrt(r^2 + h^2) + 3r + 2h]` है।
एक बेलनाकार बर्तन, जिसकी तली में अर्धगोलाकार भाग आकृति में दर्शाए अनुसार ऊपर की ओर उठा हुआ है, की धारिता `(πr^2)/3[3h - 2r]` है।
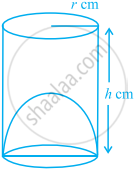
दो सर्वसम घनों, जिनमें से प्रत्येक का आयतन 64cm3 है, को सिरे से सिरा मिला कर जोड़ा जाता है। इस प्रकार प्राप्त घनाभ का पृष्ठीय क्षेत्रफल क्या है?
समान आधार त्रिज्या 8 cm और समान ऊँचाई 15 cm वाले दो शंकुओं को उनके आधारों के अनुदिश जोड़ा जाता है। इस प्रकार बने आकार का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
