Advertisements
Advertisements
Question
भुजा 7 सेमी वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [उपयोग π = `22/7`]
Solution
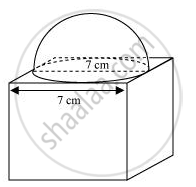
आकृति से, यह देखा जा सकता है कि इस तरह के गोलार्ध के लिए संभव सबसे बड़ा व्यास घन के किनारे के बराबर है, अर्थात् 7 सेमी।
अर्धगोलाकार भाग की त्रिज्या (r) = `7/2` = 3.5cm
ठोस का कुल पृष्ठीय क्षेत्रफल = घनीय भाग का पृष्ठीय क्षेत्रफल + अर्धगोलाकार भाग का CSA - अर्धगोलाकार भाग के आधार का क्षेत्रफल
= 6 (किनारे)2 + 2πr2 − r2
= 6 (किनारे)2 + πr2
ठोस का कुल पृष्ठीय क्षेत्रफल = `6(7)^2 + 22/7 xx 7/2xx 7/2`
= 294 + 38.5
= 332.5 सेमी2
APPEARS IN
RELATED QUESTIONS
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढ़े बने हुए हैं। घनाभ की विमाएँ 15 सेमी 10 सेमी 3.5 सेमी हैं। प्रत्येक गड्ढ़े की त्रिज्या 0.5 सेमी है और गहराई 1.4 सेमी है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए। [π = `22/7`] का प्रयोग करें।
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती है, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तंभ बना है। इस स्तंभ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है 1 घन cm3 लोहे का द्रव्यमान लगभग 8 g होता है। [उपयोग π = 3.14]
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लंबाई 8 सेमी है और व्यास 2 सेमी है जबकि गोलाकार भाग का व्यास 8.5 सेमी है। इसमें भरे जा सकने वाली पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 घन सेमी3 है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है। π = 3.14
एक 22 cm आंतरिक किनारे वाले खोखले घन को 0.5 cm व्यास वाले गोलाकार कंचों से भरा जाता है तथा यह कल्पना की जाती है कि घन का `1/8` स्थान भरा नहीं जा सकता है। तब घन में समावेशित होने वाले कंचों की संख्या ______ है।
कोई मिस्री ईंटों से विमाओं 270 cm × 300 cm × 350 cm की एक दीवार बनाता है, जिनमें से प्रत्येक ईंट की माप 22.5 cm × 11.25 cm × 8.75 cm है। यदि यह मान लिया जाए कि दीवार का `1/8` भाग मसाले से भरा जाता है, तो दीवार को बनाने में लगी ईटों की संख्या ______ है।
भुजा a वाले एक घनाकार बक्से के अंदर एक ठोस गेंद पूर्णतया ठीक-ठीक रखी जा सकती है। गेंद का आयतन `4/3πa^3` है।
एक 7 cm व्यास वाले बेलनाकार बीकर, जिसमें कुछ पानी भरा है, में 1.4 cm व्यास वाले कंचे डाले जाते हैं। कंचों की वह संख्या ज्ञात कीजिए जिनको बीकर में डालने से पानी का स्तर 5.6 cm ऊपर उठ जायेगा।
लोहे का एक खुला संदूक बनाने के लिए कितने घन सेंटीमीटर लोहे की आवश्यकता होगी, यदि इस संदूक की बाहरी विमाएँ 36 cm, 25 cm और 16.5 cm हैं, जबकि लोहे की मोटाई 1.5 cm है। यदि 1 घन सेंटीमीटर लोहे का भार 7.5 g है , तो इस संदूक का भार भी ज्ञात कीजिए।
किसी फाउन्टेन पेन की नली, जो बेलन के आकार की है, 7 cm लंबी है और इसका व्यास 5 mm है। इस पेन की नली में पूरी भरी स्याही से औसतन 3300 शब्द लिखे जा सकते हैं। स्याही की उस बोतल से कितने शब्द लिखे जा सकते हैं, जिसमें 1 लीटर की `(1)/(5)` भाग स्याही है?
