Advertisements
Advertisements
प्रश्न
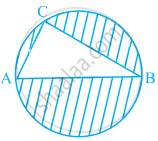
आकृति में, AB वृत का व्यास है, AC = 6 cm और BC = 8 cm है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
उत्तर
दिया गया है, AC = 6 cm और BC = 8 cm
हम जानते हैं कि कर्ण व्यास वाला अर्धवृत्त में बना त्रिभुज समकोण त्रिभुज होता है।
∴ ∠C = 90°
समकोण ΔACB में, पाइथागोरस प्रमेय का उपयोग करें,
∴ AB2 = AC2 + CB2
⇒ AB2 = 62 + 82
⇒ AB2 = 36 + 64
⇒ AB2 = 100
⇒ AB = 10 cm ...[चूँकि, भुजा ऋणात्मक नहीं हो सकती]
∴ ΔABC का क्षेत्रफल = `1/2 xx "BC" xx "AC"`
= `1/2 xx 8 xx 6`
= 24 cm2
यहाँ वृत्त का व्यास है,
AB = 10 cm
∴ वृत्त की त्रिज्या,
r = `10/2` = 5 cm
वृत्त का क्षेत्रफल = πr2
= 3.14 × (5)2
= 3.14 × 25
= 78.5 cm2
∴ छायांकित क्षेत्र का क्षेत्रफल = वृत्त का क्षेत्रफल – ΔABC का क्षेत्रफल
= 78.5 – 24
= 54.5 cm2
APPEARS IN
संबंधित प्रश्न
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
क्या यह कहना सत्य है कि व्यास d cm वाले एक वृत्ताकार पहिए द्वारा एक परिभ्रमण में चली गयी दूरी 2 π d cm होती है? क्यों?
s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
उस वृत्त की त्रिज्या ज्ञात कीजिए, जिसकी परिधि त्रिज्याओं 15 cm और 18 cm वाले दो वृत्तों की परिधियों के योग के बराबर है।
किसी ट्रैक्टर के अगले और पिछले पहियों के व्यास क्रमशः 80 cm और 2m हैं। ज्ञात कीजिए कि पिछले पहिए द्वारा उतनी दूरी तय करने में कितने चक्कर लगाने होंगे, जितनी दूरी अगला पहिया 1400 चक्कर लगाने पर तय करता है।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
आकृति में, दिये छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।