Advertisements
Advertisements
प्रश्न
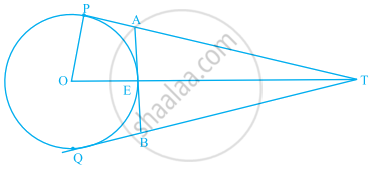
आकृति में, O त्रिज्या 5 cm वाले वृत्त का केंद्र है, T एक बिंदु इस प्रकार है कि OT = 13 cm है तथा OT वृत्त को E पर प्रतिच्छेद करती है। यदि AB, बिंदु E पर वृत्त की एक स्पर्श रेखा है तो AB की लंबाई ज्ञात कीजिए।
उत्तर
दिया गया है: केंद्र O और त्रिज्या = 5 सेमी T वाला एक वृत्त एक बिंदु है, OT = 13 सेमी। OT वृत्त को E पर काटता है और AB वृत्त की स्पर्श रेखा E पर है।
ज्ञात करना है: AB की लंबाई
OP ⊥ PT ...[वृत्त पर एक बिंदु पर स्पर्शरेखा संपर्क के बिंदु के माध्यम से त्रिज्या के लंबवत है।]
पाइथागोरस प्रमेय द्वारा ∆TOP में P पर समकोण,
(OT)2 = (OP)2 + (PT)2
(13)2 = (5)2 + (PT)2
(PT)2 = 169 – 25 = 144
PT = 12 cm
PT = TQ = 12 cm ...[बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ बराबर होती हैं।]
अब, OT = OE + ET
ET = OT – OE
= 13 – 5
= 8 cm
अब, चूँकि किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ बराबर होती हैं।
AE = PA ...[1]
EB = BQ ...[2]
साथ ही OE ⊥ AB ...[वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है।]
∠AEO = 90°
∠AEO + ∠AET = 180° ...[रैखिक युग्म द्वारा]
∠AET = 90°
ΔAET में पाइथागोरस प्रमेय द्वारा
(AT)2 = (AE)2 + (ET)2 ...[यहाँ AE = PA एक बाहरी बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ बराबर हैं।]
(PT – PA)2 = (PA)2 + (ET)2
(12 – PA)2 = (PA)2 + (8)2 ...[1 से]
144 + (PA)2 – 24PA = (PA)2 + 64
24PA = 80 ...[3]
∠AET + ∠BET = 180° ...[रैखिक युग्म]
90° + ∠BET = 180°
∠BET = 90°
ΔBET में, पाइथागोरस प्रमेय द्वारा
(BT)2 = (BE)2 + (ET)2
(TQ – BQ)2 = (BQ)2 + (ET)2 ...[2 से]
(12 – BQ)2 = (BQ)2 + (8)2
144 + (BQ)2 – 24BQ = (BQ)2 + 64
24BQ = 80 ...[4]
So, AB = AE + BE
AB = PA + BQ ...[1 और 2 से]
AB = `10/3 + 10/3` ...[3 और 4 से]
AB = `20/3` cm
APPEARS IN
संबंधित प्रश्न
आकृति में, AT केंद्र O वाले वृत्त पर एक स्पर्श रेखा इस प्रकार है कि OT = 4 cm और ∠OTA = 30° है। तब, AT बराबर ______ है।

दो संकेंद्रीय वृत्तों में से बाहरी वृत्त की त्रिज्या 5 cm है तथा इसकी 8 cm लंबी जीवा AC आंतरिक वृत्त की स्पर्श रेखा है। आंतरिक वृत्त की त्रिज्या ज्ञात कीजिए।
उपरोक्त प्रश्न 5 में, यदि दोनों वृत्तों की त्रिज्याएँ बराबर हों, तो सिद्ध कीजिए कि AB = CD है।
एक वृत्त की जीवा PQ, बिंदु R पर इस वृत्त की स्पर्श रेखा के समांतर है। सिद्ध कीजिए कि बिंदु R चाप PRQ को समद्विभाजित करता है।
सिद्ध कीजिए कि किसी वृत्त की एक जीवा के सिरों पर खींची गई स्पर्श रेखाएँ उस जीवा से बराबर कोण बनाती हैं।
सिद्ध कीजिए कि किसी वृत्त का एक व्यास AB उन सभी जीवाओं को समद्विभाजित करता है, जो बिंदु A से खींची गई वृत्त की स्पर्श रेखा के समांतर हैं।
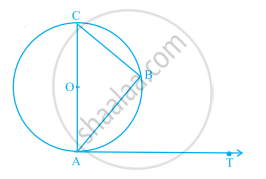
यदि केंद्र O वाले वृत्त की AB एक जीवा है, AOC एक व्यास है तथा AT बिंदु A पर खींची गई स्पर्श रेखा है, जैसा कि आकृति में दर्शाया गया है। सिद्ध कीजिए कि ∠BAT = ∠ACB है।
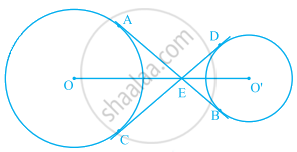
आकृति में, केंद्रों O और O' वाले दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ AB और CD परस्पर E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि बिंदु O, E, O' संरेखी हैं।
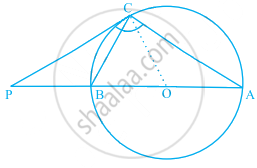
किसी वृत्त की बिंदु C पर खींची गई स्पर्श रेखा और व्यास AB बढ़ाने पर बिंदु P पर प्रतिच्छेद करते हैं। यदि ∠PCA = 110° है, तो ∠CBA ज्ञात कीजिए।
यदि त्रिज्या 9 cm वाले एक वृत्त के अंतर्गत एक समद्विबाहु त्रिभुज ABC खींचा गया है, जिसमें AB = AC = 6 cm है, तो उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
