Advertisements
Advertisements
प्रश्न
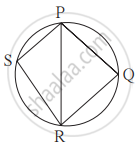
आकृति में, `square`PQRS एक चक्रीय चतुर्भुज है। भुजा PQ ≅ भुजा RQ, ∠PSR = 110°, तो
(1) ∠PQR = कितना?
(2) m(चाप PQR) = कितना?
(3) m(चाप QR) = कितना?
(4) ∠PRQ = कितना?
उत्तर
(1) `square`PQRS एक चक्रीय चतुर्भुज है। .............(दिया है)
∠PSR + ∠PQR = 180° ........(चक्रीय चतुर्भुज का सम्मुख कोण)
∴ 110° + ∠PQR = 180°
∴ ∠PQR = 180° - 110°
∴ ∠PQR = 70°
(2) ∠PSR = `1/2`m(चाप PQR) ........(अंतर्लिखित कोण का प्रमेय)
∴ 110° = `1/2`m(चाप PQR)
∴ m(चाप PQR) = 110° × 2
∴ m(चाप PQR) = 220°.
(3) जीवा PQ ≅ जीवा QR .................(दिया है)
∴ चाप PQ ≅ चाप QR ...............(सर्वांगसम जीवाओं के संगत चाप)
मानो m(चाप PQ) = m(चाप QR) = x
m(चाप PQ) + m(चाप QR) = m(चाप PQR) ........(चापों का योग गुणधर्म)
∴ x + x = 220°
∴ 2x = 220°
∴ x = `(220°)/2`
∴ x = 110°
∴ m(चाप QR) = 110° और m(चाप PQ) = 110°
(4) ∠PRQ = `1/2`m(चाप PQ) .............(अंतर्लिखित कोण का प्रमेय)
∴ ∠PRQ = `1/2 xx 110^circ`
∴ ∠PRQ = 55°
(1) ∠PQR = 70°
(2) m(चाप PQR) = 220°
(3) m(चाप QR) = 110°
(4) ∠PRQ = 55°
APPEARS IN
संबंधित प्रश्न
चक्रीय `square`MRPN में, ∠R = (5x - 13)° और ∠N = (4x + 4)°, तो ∠R और ∠N के माप ज्ञात कीजिए।
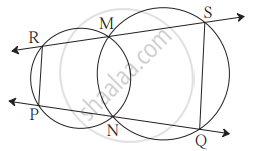
आकृति में, दो वृत्त एक दूसरे को बिंदु M तथा N पर प्रतिच्छेदित करते हैं। यदि बिंदु M तथा N से खींची गई वृत्त की छेदन रेखाएँ वृत्तों के क्रमशः बिंदु R तथा S पर तथा बिंदु P तथा Q पर प्रतिच्छेदित करती हों तो सिद्ध कीजिए कि PR || QS
सिद्ध करो: ''चक्रीय चतुर्भुज के सम्मुख कोण परस्पर संपूरक होते हैं।''
