Advertisements
Advertisements
प्रश्न
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
उत्तर
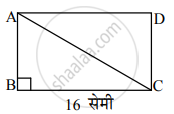
समजा, `square`ABCD हा आयत आहे.
BC = 16 सेमी
आयताचे क्षेत्रफळ = लांबी × रुंदी
`square`ABCD चे क्षेत्रफळ = BC × AB
∴ 192 = 16 × AB
∴ AB = `192/16`
= 12 सेमी
आता, ΔABC मध्ये, ∠B = 90° ...[आयताचा कोन]
∴ AC2 = AB2 + BC2 ....[पायथागोरसचे प्रमेय]
= 122 + 162
= 144 + 256
= 400
∴ AC = `sqrt400` ...[दोन्ही बाजूंचे वर्गमूळ घेऊन]
= 20 सेमी
∴ आयताच्या कर्णाची लांबी 20 सेमी आहे.
APPEARS IN
संबंधित प्रश्न
एका चौरसाचा कर्ण 10 सेमी आहे तर त्याच्या बाजूची लांबी व परिमिती काढा.
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
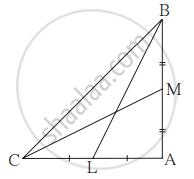
ΔABC मध्ये ∠BAC = 90°, रेख BL व रेख CM या ΔABC च्या मध्यगा आहेत, तर सिद्ध करा : 4(BL2 + CM2 ) = 5BC2.
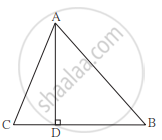
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये कर्णाची लांबी 25 सेमी व उंची 7 सेमी असेल, तर त्याच्या पायाची लांबी काढा.
∆LMN मध्ये, l = 5, m = 13, n = 12, तर ∆LMN हा काटकोन त्रिकोण आहे किंवा नाही ते ठरवण्यासाठी कृती करा. [l, m, n या ∠L, ∠M, व ∠N यांच्या समोरील बाजू आहेत.]
कृती: ∆LMN मध्ये, l = 5, m = 13, n = `square`
l2 = `square`, m2 = 169; n2 = 144.
l2 + n2 = 25 + 144 = `square`
`square^2` + l2 = m2
∴ पायथागोरसच्या प्रमेयानुसार, ∆LMN हा काटकोन त्रिकोण आहे.
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
एका चौरसाचा कर्ण `10sqrt2` सेमी असतील तर त्याच्या बाजूची लांबी काढा.
