Advertisements
Advertisements
प्रश्न
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। तब, ar (BDE) = `1/4` ar (ABC) है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
दिया गया है - ΔABC और ΔBDE दो समबाहु त्रिभुज हैं।
मान लीजिए कि त्रिभुज ABC की प्रत्येक भुजा x है।
इसी प्रकार, D, BC का मध्य-बिंदु है।
इसलिए, त्रिभुज BDE की प्रत्येक भुजा `x/2` है।
अब, `("क्षेत्रफल"(Δ"BDE"))/("क्षेत्रफल"(Δ"ABC")) = (sqrt(3)/4 xx (x/2)^2)/(sqrt(3) / 4 xx x^2)`
= `x^2/(4x^2)`
= `1/4`
इसलिए, क्षेत्रफल (ΔBDE) = `1/4` क्षेत्रफल (ΔABC)।
APPEARS IN
संबंधित प्रश्न
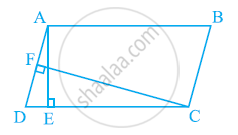
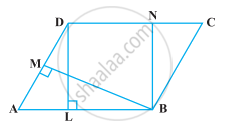
दी गई आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
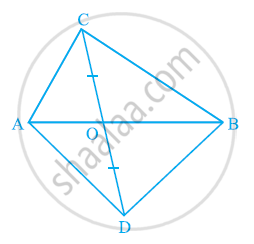
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
एक समलंब ABCD, जिसमें AB || DC हैं, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दर्शाइए कि ar(AOD) = ar(BOC) है |
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप इस प्रश्न का उत्तर दे सकते हैं कि आपने इस अध्याय के 'परिचय' में छोड़ दिया है कि "क्या बुधिया के खेत को वास्तव में बराबर क्षेत्रफल के तीन भागों में बांटा गया है"?
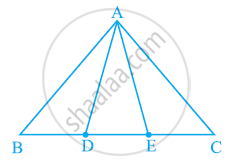
[टिप्पणी: ध्यान दें कि BD = DE = EC लेने पर त्रिभुज ABC को बराबर क्षेत्रफलों वाले तीन त्रिभुज ABD, ADE और AEC में विभाजित किया जाता है। इसी तरह, BC को n समान भागों में विभाजित करके और इस प्रकार प्राप्त विभाजन बिंदुओं को BC के विपरीत शीर्ष से जोड़कर, आप ΔABC को समान क्षेत्रफल वाले n त्रिभुजों में विभाजित कर सकते हैं।]
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
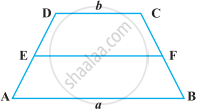
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = b cm है (आकृति)। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात हैं
PQRS एक आयत है, जो त्रिज्या 13 cm वाले एक वृत्त के चतुर्थांश के अंतर्गत है। A भुजा PQ पर स्थित कोई बिंदु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm2 है।
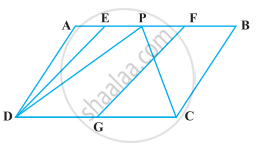
निम्नलिखित आकृति में, ABCD और EFGD समांतर चतुर्भुज हैं तथा G भुजा CD का मध्य-बिंदु है। तब, ar (DPC) = `1/2` ar (EFGD) है।
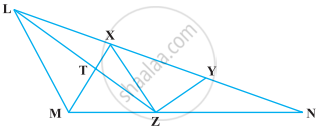
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।