Advertisements
Advertisements
प्रश्न
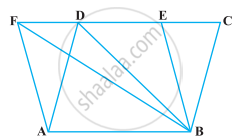
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = b cm है (आकृति)। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात हैं
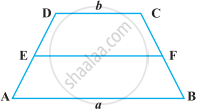
पर्याय
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
उत्तर
(3a + b) : (a + 3b)
स्पष्टीकरण -
दिया गया है, AB = a cm, DC = b cm और AB || DC।
साथ ही, E और F क्रमश : AD और BC के मध्य-बिंदु हैं।
तो, CD, EF और AB, EF के बीच की दूरी समान होगी, मान लीजिए h।

BD को मिलाइए जो EF को M पर प्रतिच्छेद करती है।
अब, ΔABD में, AD और EM || AB का मध्य-बिंदु E है।
तो, M, BD का मध्य-बिंदु है।
और EM = `1/2` AB [मध्य-बिंदु प्रमेय द्वारा] ...(i)
इसी प्रकार ΔCBD में, MF = `1/2`CD ...(ii)
समीकरण (i) और (ii) को जोड़ने पर, हम पाते हैं।
EM + MF = `1/2` AB + `1/2` CD
⇒ EF = `1/2`(AB + CD) = `1/2`(a + b)
अब, समलंब ABFE का क्षेत्रफल
= `1/2` (समांतर भुजाओं का योग) × (समानांतर भुजाओं के बीच की दूरी)
= `1/2(a + 1/2(a + b)) xx h`
= `1/4(3a + b)h`
अब, समलंब EFCD का क्षेत्रफल
= `1/2[b + 1/2(a + b)] xx h`
= `1/4(3b + a)h`
∴ आवश्यक अनुपात = `"ABFE का क्षेत्रफल"/"EFCD का क्षेत्रफल"`
= `(1/4(3a + b)h)/(1/4(3b + a)h)`
= `((3a + b))/((a + 3b))` या (3a + b) : (a + 3b)
APPEARS IN
संबंधित प्रश्न
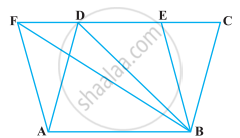
D, E और F क्रमशः ΔABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। वो दिखाओ
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (DEF) = `1/4`ar (ABC)
(iii) ar (BDEF) = `1/2`ar (ABC)
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है | यदि BE || AC और CF || AB रेखा XY से क्रमश: E और F पर मिलती है, तो दर्शाइए कि:
ar(ABE) = ar(ACF)
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त करते हैं :
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल है :
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
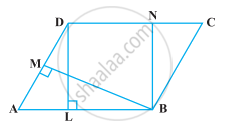
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए :
ar (ΔABD)
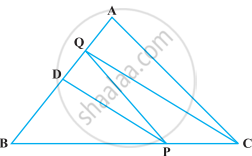
∆ABC, D भुजा AB का मध्य-बिंदु है तथा P भुजा BC पर स्थित कोई बिंदु है। यदि रेखाखंड CQ || PD भुजा AB से Q पर मिलता है (आकृति), तो सिद्ध कीजिए कि ar (BPQ) = `1/2` ar (∆ABC) है।