Advertisements
Advertisements
प्रश्न
ABCD एक समांतर चतुर्भुज और X भुजा AB का मध्य-बिंदु है। यदि ar (AXCD) = 24 cm2 है तो ar (ABC) = 24 cm2 है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन असत्य है।
स्पष्टीकरण -
प्रश्न में दिया गया है, ABCD एक समांतर चतुर्भुज है और X AB का मध्य-बिंदु है।
इसलिए, क्षेत्रफल (ABCD) = क्षेत्रफल (AXCD) + क्षेत्रफल (ΔXBC) ...(i)
अब, समांतर चतुर्भुज का विकर्ण AC इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है।
क्षेत्रफल (ABCD) = 2 क्षेत्रफल (ΔABC) ...(ii)
इसी प्रकार, X, AB का मध्य-बिंदु है,
इसलिए, क्षेत्रफल(ΔCXB) = `1/2` क्षेत्रफल (ABC) ...(iii) [माध्यिका त्रिभुज को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।]
2 क्षेत्रफल (ΔABC) = `24 + 1/2` क्षेत्रफल (ΔABC) ...[समीकरण (i), (ii) और (iii) का प्रयोग करके]
अब, 2 क्षेत्रफल (ΔABC) – `1/2` क्षेत्रफल (ΔABC) = 24
`3/2` क्षेत्रफल (ΔABC) = 24
इसलिए, क्षेत्र(ΔABC) = `(2 xx 24)/3` = 16 cm2
APPEARS IN
संबंधित प्रश्न
निम्नलिखित में से कौन सी आकृति एक ही आधार पर और समान समांतर रेखाओं के बीच स्थित है? ऐसी स्थिति में उभयनिष्ठ आधार और दो समांतर रेखाएँ लिखिए।
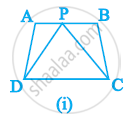
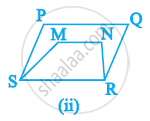
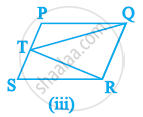

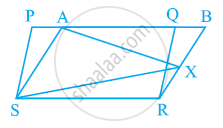
दी गई आकृति में, PQRS और ABRS समांतर चतुर्भुज हैं और X भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = `1/2` ar (PQRS)
एक त्रिभुज की माध्यिका उसे विभाजित करती है, दो ______।
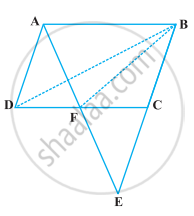
ABCD एक समांतर चतुर्भुज है, जिसमें BC को E तक इस प्रकार बढ़ाया गया है कि CE = BC है (आकृति)। AE भुजा CD को F पर प्रतिच्छेद करती है। यदि ar (DFB) = 3 cm2 है, तो समांतर चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।