Advertisements
Advertisements
प्रश्न
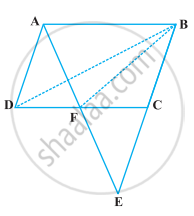
ABCD एक समांतर चतुर्भुज है, जिसमें BC को E तक इस प्रकार बढ़ाया गया है कि CE = BC है (आकृति)। AE भुजा CD को F पर प्रतिच्छेद करती है। यदि ar (DFB) = 3 cm2 है, तो समांतर चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
उत्तर
दिया गया है - ABCD एक समांतर चतुर्भुज है जिसमें BC को E तक इस प्रकार बढ़ाया गया है कि CE = BC है। C, BE का मध्य-बिंदु है और ar (ΔDFB) = 3 सेमी2 है।
त्रिभुज ADF और त्रिभुज EFC में,
∠DAF = ∠CEF ...[वैकल्पिक आंतरिक कोण]
AD = CE ...[AD = BC = CE]
∠ADF = ∠FCE ...[वैकल्पिक आंतरिक कोण]
इसलिए, ΔADF ≅ ΔECF ...[सर्वांगसमता के SAS नियम द्वारा]
अब, ΔADF ≅ ΔECF ...[सर्वांगसमता के SAS नियम द्वारा]
DF = CF ...[CPCT]
चूँकि BF, त्रिभुज BCD की माध्यिका है।
ar (ΔBDF) = `1/2` ar (BCD) ...(i) [माध्यिका त्रिभुज को समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।]
जैसा कि हम जानते हैं कि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और समान समांतर रेखाओं के बीच होते हैं, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल के आधे के बराबर होता है।
ar (ΔBCD) = `1/2` ar (ABCD) ...(ii)
ar (ΔBDF) = `1/2 {1/2 "ar" ("ABCD")}` ...[समीकरण (i) द्वारा]
3 cm2 = `1/4` ar (ABCD)
ar (ABCD) = 12 सेमी2
अत:, समांतर चतुर्भुज का क्षेत्रफल 12 सेमी2 है।
APPEARS IN
संबंधित प्रश्न
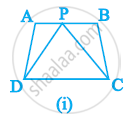
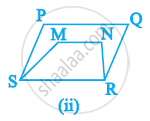
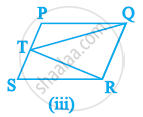
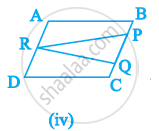
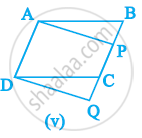
निम्नलिखित में से कौन सी आकृति एक ही आधार पर और समान समांतर रेखाओं के बीच स्थित है? ऐसी स्थिति में उभयनिष्ठ आधार और दो समांतर रेखाएँ लिखिए।

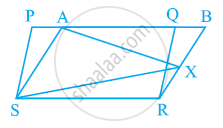
दी गई आकृति में, PQRS और ABRS समांतर चतुर्भुज हैं और X भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = `1/2` ar (PQRS)
एक त्रिभुज की माध्यिका उसे विभाजित करती है, दो ______।
ABCD एक समांतर चतुर्भुज और X भुजा AB का मध्य-बिंदु है। यदि ar (AXCD) = 24 cm2 है तो ar (ABC) = 24 cm2 है।
