Advertisements
Advertisements
प्रश्न
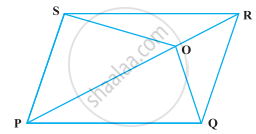
O एक समांतर चतुर्भुज PQRS के विकर्ण PR पर स्थित कोई बिंदु है (आकृति)। सिद्ध कीजिए कि ar (PSO) = ar (PQO) है।
उत्तर
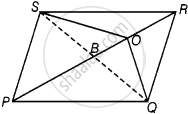
दिया गया है - एक समांतर चतुर्भुज PQRS में, O विकर्ण PR पर कोई बिंदु है।
सिद्ध करना है - ar (ΔPSO) = ar (ΔPQO)
रचना - SQ को मिलाइए जो PR को B पर प्रतिच्छेद करती है।
उपपत्ति - हम जानते हैं कि, समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं, इसलिए B, SQ का मध्य-बिंदु है।
यहाँ, PB, ΔQPS की एक माध्यिका है और हम जानते हैं कि, एक त्रिभुज की एक माध्यिका इसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
∴ ar (ΔBPQ) = ar (ΔBPS) ...(i)
साथ ही, OB, ∆OSQ की माध्यिका है।
∴ ar (ΔOBQ) = ar (ΔOBS) ...(ii)
समीकरण (i) और (ii) को जोड़ने पर, हम पाते हैं।
ar (ΔBPQ) + ar (ΔOBQ) = ar (ΔBPS) + ar (ΔOBS)
⇒ ar (ΔPQO) = ar (ΔPSO)
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं | यदि रेखाखंड CD रेखाखंड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है
ABCD एक समलंब है, जिसमें AB || DC है और AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है | सिद्ध कीजिए कि ar (ADX) = ar (ACY) है |
[संकेत : CX को मिलाइए]
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिंदुओं को मिलाने से बनी आकृति है :
निम्नलिखित आकृति में, यदि समांतर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल के हैं, तो ______।
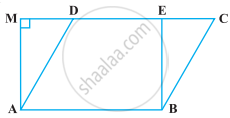
एक त्रिभुज की भुजाओं के मध्य-बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD ______।
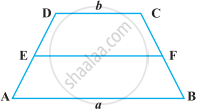
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = b cm है (आकृति)। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात हैं
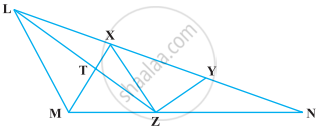
X और Y त्रिभुज LMN की भुजा LN पर स्थित दो बिंदु इस प्रकार हैं कि LX = XY = YN हैं। X से होकर जाती हुई एक रेखा LM के समांतर खींची गई जो MN को Z पर मिलती है। (देखिए आकृति)। सिद्ध कीजिए कि ar (LZY) = ar (MZYX) है।
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है (आकृति)। ज्ञात कीजिए :
- ar (ABEF)
- ar (ABD)
- ar (BEF)