Advertisements
Advertisements
प्रश्न
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
उत्तर
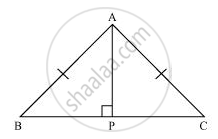
दिया गया है: ABC एक समद्विबाहु त्रिभुज है
जिसमें AB = AC
सिद्ध करना है: ∠B = ∠C
रचना: AP ⊥ BC खींचिए।
उपपत्ति: ∆ABP और ∆ACP में,
∠APB = ∠APC ...(प्रत्येक 90°) ...(रचना से)
AB = AC ...(दिया गया है)
AP = AP ...(उभयनिष्ठ)
ΔABP ≅ ΔACP ...(RHS सर्वांगसमता नियम से)
अतः, ∠B = ∠C ...(सर्वांगसम त्रिभुजों के संगत भाग)
APPEARS IN
संबंधित प्रश्न
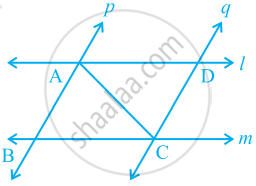
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
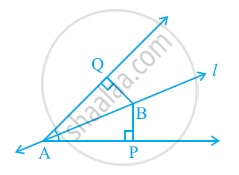
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
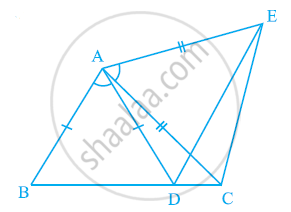
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
यदि ∆PQR ≅ ∆EDF है, तो क्या यह कहना सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
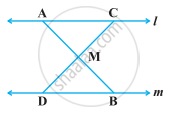
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिंदु M तक बढ़ाया जाता है। सिद्ध कीजिए कि ∠MOC = ∠ABC है।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
