Advertisements
Advertisements
प्रश्न
उत्तर
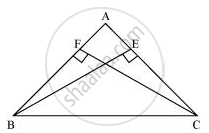
ΔBEC और ΔCFB में,
∠BEC = ∠CFB ...(प्रत्येक 90°)
BC = CB ...(उभयनिष्ठ)
BE = CF ...(दिया गया है)
∴ ΔBEC ≅ ΔCFB ...(RHS सर्वांगसमता नियम द्वारा)
⇒ ∠BCE = ∠CBF ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा)
अब, ΔABC में, ∠BCA = ∠CBA
∴ AB = AC ...(एक त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं)
अत:, ΔABC समद्विबाहु है।
APPEARS IN
संबंधित प्रश्न
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
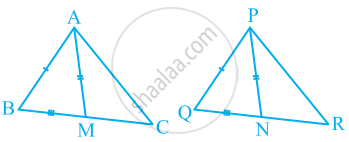
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
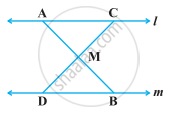
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
