Advertisements
Advertisements
प्रश्न
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
उत्तर
दिया गया है - चतुर्भुज ABCD में, AB = AD और CB = CD है।
रचना - AC और BD को मिलाइए।
सिद्ध करना है - AC, BD का लम्ब समद्विभाजक है।
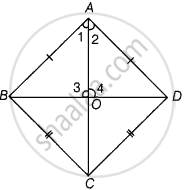
प्रमाण - ΔABC और ΔADC में,
AB = AD ...[दिया गया है।]
BC = CD ...[दिया गया है।]
और AC = AC ...[उभयनिष्ठ पक्ष]
∴ ΔABC ≅ ΔADC ...[SSS सर्वांगसमता नियम द्वारा]
⇒ ∠1 = ∠2 ...[CPCT द्वारा]
अब, ∆AOB और ΔAOD में,
AB = AD ...[दिया गया है।]
⇒ ∠1 = ∠2 ...[ऊपर सिद्ध]
और AO = AO ...[उभयनिष्ठ पक्ष]
∴ ΔAOB ≅ ΔAOD ...[SAS सर्वांगसमता नियम द्वारा]
⇒ BO = DO ...[CPCT द्वारा]
और ∠3 = ∠4 [CPCT द्वारा] ...(i)
लेकिन ∠3 + ∠4 = 180° ...[रैखिक युग्म अभिगृहीत]
∠3 + ∠3 = 180° ...[समीकरण (i) से]
⇒ 2∠3 = 180°
⇒ ∠3 = `(180^circ)/2`
∴ ∠3 = 90°
अर्थात्, AC, BD का लम्ब समद्विभाजक है।
APPEARS IN
संबंधित प्रश्न
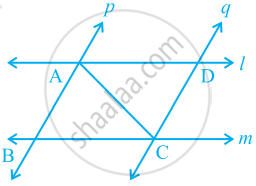
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
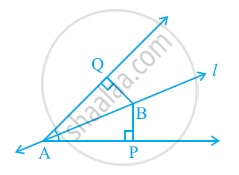
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA < 2(BD + AC) होता है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
