Advertisements
Advertisements
प्रश्न
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
उत्तर
दिया गया है - दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं और O से होकर जाने वाली रेखा n पर एक बिंदु P इस प्रकार है कि P, l और m से समदूरस्थ है, अर्थात, PQ = PR।
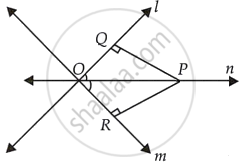
सिद्ध करना है - n, l और m द्वारा बने कोण का समद्विभाजक है अर्थात n, ∠QOR का समद्विभाजक है।
प्रमाण - ΔOQP और ΔORP में,
∠PQO = ∠PRO = 90° ...[चूँकि, P, l और m से समान दूरी पर है, इसलिए PQ और PR क्रमशः l और m रेखाओं के लंबवत होने चाहिए]
OP = OP ...[उभयनिष्ठ पक्ष]
PQ = PR ...[दिया गया है।]
∴ ΔOQP ≅ ΔORP ...[RHS सर्वांगसमता नियम द्वारा]
⇒ ∠POQ = ∠POR ...[CPCT द्वारा]
अतः, n, ∠QOR का समद्विभाजक है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
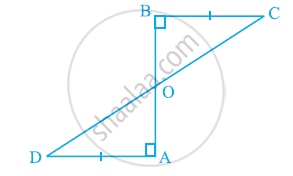
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
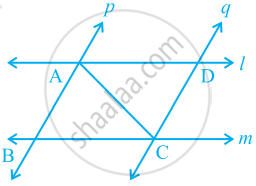
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
यदि ∆PQR ≅ ∆EDF है, तो क्या यह कहना सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
