Advertisements
Advertisements
प्रश्न
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
उत्तर
दिया गया है - चतुर्भुज ABCD में, AB = AD और CB = CD है।
रचना - AC और BD को मिलाइए।
सिद्ध करना है - AC, BD का लम्ब समद्विभाजक है।
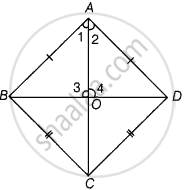
प्रमाण - ΔABC और ΔADC में,
AB = AD ...[दिया गया है।]
BC = CD ...[दिया गया है।]
और AC = AC ...[उभयनिष्ठ पक्ष]
∴ ΔABC ≅ ΔADC ...[SSS सर्वांगसमता नियम द्वारा]
⇒ ∠1 = ∠2 ...[CPCT द्वारा]
अब, ∆AOB और ΔAOD में,
AB = AD ...[दिया गया है।]
⇒ ∠1 = ∠2 ...[ऊपर सिद्ध]
और AO = AO ...[उभयनिष्ठ पक्ष]
∴ ΔAOB ≅ ΔAOD ...[SAS सर्वांगसमता नियम द्वारा]
⇒ BO = DO ...[CPCT द्वारा]
और ∠3 = ∠4 [CPCT द्वारा] ...(i)
लेकिन ∠3 + ∠4 = 180° ...[रैखिक युग्म अभिगृहीत]
∠3 + ∠3 = 180° ...[समीकरण (i) से]
⇒ 2∠3 = 180°
⇒ ∠3 = `(180^circ)/2`
∴ ∠3 = 90°
अर्थात्, AC, BD का लम्ब समद्विभाजक है।
APPEARS IN
संबंधित प्रश्न
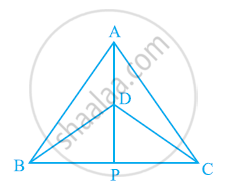
△ABC और △DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि:
- △ABD ≌ △ACD
- △ABP ≌ △ACP
- AP कोण A और कोण D दोनों को समद्विभाजित करता है।
- AP रेखाखंड BC का लम्ब समद्विभाजक है।
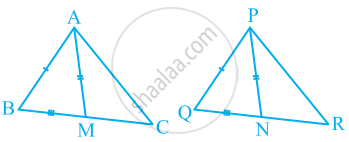
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
