Advertisements
Advertisements
प्रश्न
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
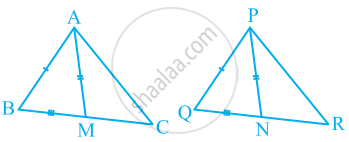
उत्तर
ΔABC में, AM, BC की माध्यिका है।
∴ BM = `1/2 BC`
ΔPQR में, PN, QR की माध्यिका है।
∴ QN = `1/2QR`
हालाँकि, BC = QR
∴ `1/2BC` = `1/2QR`
⇒ BM = QN …(1)
(i) ΔABM और ΔPQN में,
AB = PQ ...(दिया गया है)
BM = QN ...[समीकरण (1) से]
AM = PN ...(दिया गया है)
∴ ΔABM ≅ ΔPQN ...(SSS सर्वांगसमता नियम)
∠ABM = ∠PQN ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा)
∠ABC = ∠PQR …(2)
(ii) ΔABC और ΔPQR में,
AB = PQ ...(दिया गया है)
∠ABC = ∠PQR ...[समीकरण (2) से]
BC = QR ...(दिया गया है)
⇒ ΔABC ≅ ΔPQR ...(SAS सर्वांगसमता नियम से)
APPEARS IN
संबंधित प्रश्न
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
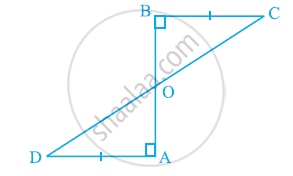
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
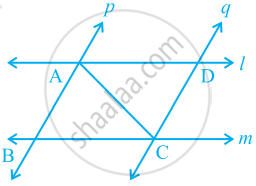
△ABC और △DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि:
- △ABD ≌ △ACD
- △ABP ≌ △ACP
- AP कोण A और कोण D दोनों को समद्विभाजित करता है।
- AP रेखाखंड BC का लम्ब समद्विभाजक है।
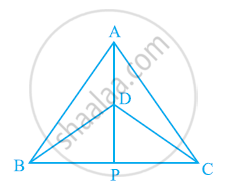
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन-सी भुजा ∆ABC की भुजा BC के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
