Advertisements
Advertisements
प्रश्न
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन-सी भुजा ∆ABC की भुजा BC के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
उत्तर
दिया गया है - त्रिभुज ABC और PQR में,
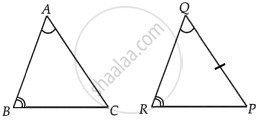
∠A = ∠Q और ∠B = ∠R ...[दिया गया है।]
BC = RP ...[त्रिभुज के सर्वांगसम होने के लिए]
अत:, यह AAS सर्वांगसम नियम द्वारा सर्वांगसम होगा।
APPEARS IN
संबंधित प्रश्न
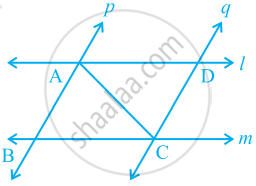
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
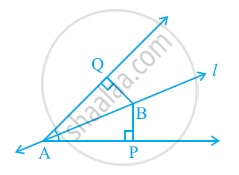
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
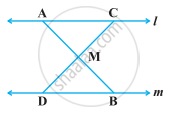
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
