Advertisements
Advertisements
प्रश्न
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
उत्तर
दिया गया है - समलंब ABCD में, बिंदु M और N क्रमशः समानांतर भुजाओं AB और DC के मध्य-बिंदु हैं और MN को मिलाते हैं, जो AB और DC के लंबवत है।
सिद्ध करना है - AD = BC
उपपत्ति - चूँकि M, AB का मध्य-बिंदु है।
∴ AM = MB
अब, ΔAMN और ΔBMN में,
AM = MB ...[ऊपर प्रमाणित]
∠3 = ∠4 ...[प्रत्येक 90°]
MN = MN ...[उभयनिष्ठ पक्ष]
∴ ΔAMN ≅ ΔBMN ...[SAS सर्वांगसमता नियम द्वारा]
∴ ∠1 = ∠2 ...[CPCT द्वारा]
उपरोक्त समीकरण के दोनों पक्षों को –1 से गुणा करने पर और फिर दोनों पक्षों में 90° जोड़ने पर, हमें प्राप्त होता है।
90° – ∠1 = 90° – ∠2
⇒ ∠AND = ∠BNC ...(i)
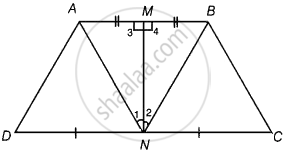
अब, ΔADN और ΔBCN में,
∠AND = ∠BNC ...[समीकरण (i) से]
AN = BN ...[∵ΔAMN ≅ ΔBMN]
और DN = NC ...[∵ N, CD का मध्य-बिंदु है (दिया गया है।)]
∴ ΔADN ≅ ΔBCN ...[SAS सर्वांगसमता नियम द्वारा]
अतः, AD = BC ...[CPCT द्वारा]
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
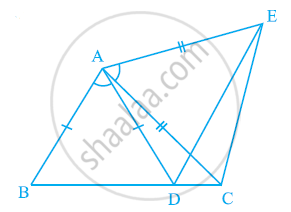
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
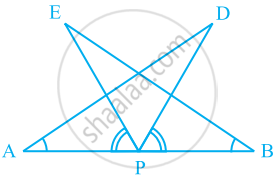
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
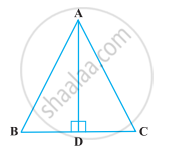
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA < 2(BD + AC) होता है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
