Advertisements
Advertisements
Question
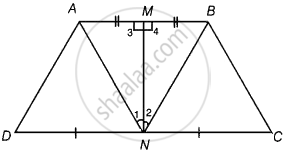
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
Solution
दिया गया है - समलंब ABCD में, बिंदु M और N क्रमशः समानांतर भुजाओं AB और DC के मध्य-बिंदु हैं और MN को मिलाते हैं, जो AB और DC के लंबवत है।
सिद्ध करना है - AD = BC
उपपत्ति - चूँकि M, AB का मध्य-बिंदु है।
∴ AM = MB
अब, ΔAMN और ΔBMN में,
AM = MB ...[ऊपर प्रमाणित]
∠3 = ∠4 ...[प्रत्येक 90°]
MN = MN ...[उभयनिष्ठ पक्ष]
∴ ΔAMN ≅ ΔBMN ...[SAS सर्वांगसमता नियम द्वारा]
∴ ∠1 = ∠2 ...[CPCT द्वारा]
उपरोक्त समीकरण के दोनों पक्षों को –1 से गुणा करने पर और फिर दोनों पक्षों में 90° जोड़ने पर, हमें प्राप्त होता है।
90° – ∠1 = 90° – ∠2
⇒ ∠AND = ∠BNC ...(i)
अब, ΔADN और ΔBCN में,
∠AND = ∠BNC ...[समीकरण (i) से]
AN = BN ...[∵ΔAMN ≅ ΔBMN]
और DN = NC ...[∵ N, CD का मध्य-बिंदु है (दिया गया है।)]
∴ ΔADN ≅ ΔBCN ...[SAS सर्वांगसमता नियम द्वारा]
अतः, AD = BC ...[CPCT द्वारा]
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
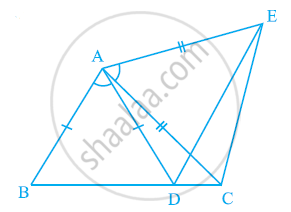
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
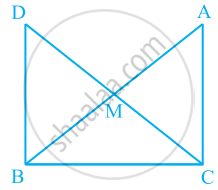
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिंदु M तक बढ़ाया जाता है। सिद्ध कीजिए कि ∠MOC = ∠ABC है।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिंदु है ताकि BD = `1/2` AC है। दर्शाइए कि ∠ABC एक समकोण है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
