Advertisements
Advertisements
Question
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिंदु M तक बढ़ाया जाता है। सिद्ध कीजिए कि ∠MOC = ∠ABC है।
Solution
प्रश्न में दिया गया है, AB = AC वाले समद्विबाहु त्रिभुज ABC के कोण B और C के समद्विभाजक एक दूसरे को O पर काटते हैं। अब BO को बिंदु M तक बढ़ाया गया है।
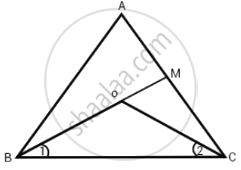
त्रिभुज ABC में,
AB = AC
∠ABC = ∠ACB ...[त्रिभुज की समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
`1/2 ∠ABC = 1/2 ∠ACB`
अर्थात् ∠1 = ∠2 ...[चूँकि, BO और CO ∠B और ∠C के समद्विभाजक हैं।]
त्रिभुज OBC में,
बाहरी ∠MOC = ∠1 + ∠2 ...[त्रिभुज का बाह्य कोण आंतरिक विपरीत कोणों के योग के बराबर होता है।]
बाहरी ∠MOC = 2∠1 ...[∠1 = ∠2]
अतः, ∠MOC = ∠ABC
APPEARS IN
RELATED QUESTIONS
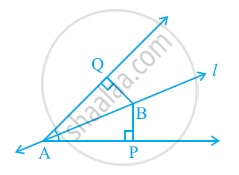
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
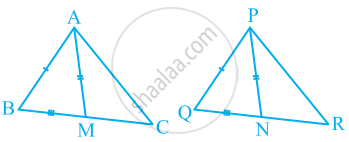
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
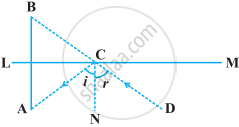
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
