Advertisements
Advertisements
Question
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
Solution
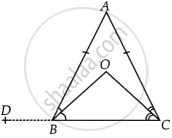
दिया गया है - ΔABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC, BO और CO क्रमश: ∠ABC और ∠ACB के समद्विभाजक हैं जो O पर प्रतिच्छेद करते हैं।
दिखाएँ के लिए - ∠DBA = ∠BOC
उत्पादन - रेखा CB का उत्पादन D पर किया गया था।
उपपत्ति - ΔABC में, AB = AC ...[दिया गया है।]
∠ACB = ∠ABC ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
⇒ `1/2 ∠ACB = 1/2 ∠ABC` ...[दोनों पक्षों को 2 से भाग देने पर]
⇒ ∠OCB = ∠OBC ...(i) [∵ BO और CO, ∠ABC और ∠ACB के समद्विभाजक हैं।]
∆BOC में, ∠OBC + ∠OCB + ∠BOC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠OBC + ∠OBC + ∠BOC = 180° ...[समीकरण (i) से]
⇒ 2∠OBC + ∠BOC = 180°
⇒ ∠ABC + ∠BOC = 180° ...[∵ BO, ∠ABC का समद्विभाजक है।]
⇒ 180° – ∠DBA + ∠BOC = 180° ...[∵ DBC एक सरल रेखा है।]
⇒ – ∠DBA + ∠BOC = 0
⇒ ∠DBA = ∠BOC
APPEARS IN
RELATED QUESTIONS
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
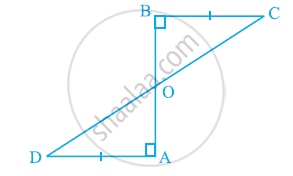
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
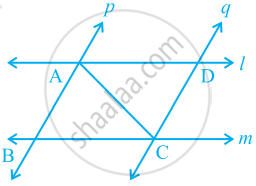
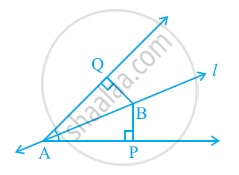
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
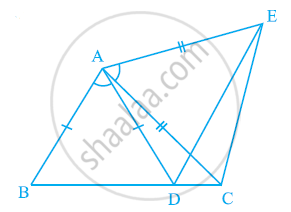
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
यदि ∆PQR ≅ ∆EDF है, तो क्या यह कहना सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
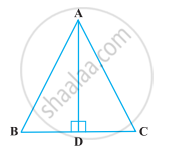
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
