Advertisements
Advertisements
Question
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
Solution
हमने ΔABC दिया है जो एक समद्विबाहु समकोण त्रिभुज है जिसमें AB = AC है तथा AD, ∠A का समद्विभाजक है।
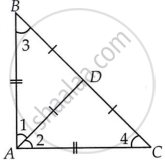
अब ΔABC में,
AB = AC ...[दिया गया है।]
⇒ ∠C = ∠B ...(1) [बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
अब, ΔABC में, ∠A = 90°
∠A + ∠B + ∠C = 180° ...[Δ का कोण योग गुण]
⇒ 90° + ∠B + ∠B = 180° ...[(1) से]
⇒ 2∠B = 90°
⇒ ∠B = 45°
⇒ ∠B = ∠C = 45° or ∠3 = ∠4 = 45°
साथ ही, ∠1 = ∠2 = 45° ...[∵ AD, ∠A का समद्विभाजक है।]
साथ ही, ∠1 = ∠3, ∠2 = ∠4 = 45°
⇒ BD = AD, DC = AD ...(2) [बराबर कोणों के विपरीत भुजाएँ बराबर होती हैं।]
इस प्रकार, BC = BD + DC = AD + AD ...[(2) से]
⇒ BC = 2AD
APPEARS IN
RELATED QUESTIONS
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
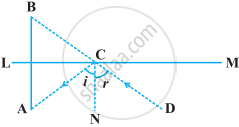
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA < 2(BD + AC) होता है।
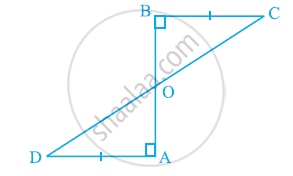
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिंदु है ताकि BD = `1/2` AC है। दर्शाइए कि ∠ABC एक समकोण है।
एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
सिद्ध कीजिए कि एक समबाहु त्रिभुज को छोड़कर, किसी त्रिभुज में सबसे लंबी भुजा का सम्मुख कोण एक समकोण के `2/3` भाग से बड़ा होता हैं।
