Advertisements
Advertisements
Question
O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
Advertisements
Solution
दिया गया है - वर्ग ABCD के अभ्यंतर में O एक बिंदु इस प्रकार है कि ΔOAB एक समबाहु त्रिभुज है।
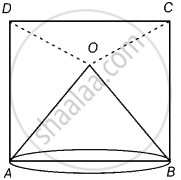
रचना - OC और OD को मिलाइए।
दर्शाना है - ΔOCD एक समद्विबाहु त्रिभुज है।
उपपत्ति - चूँकि, AOB एक समबाहु त्रिभुज है।
∴ ∠OAB = ∠OBA = 60° ...(i)
साथ ही, ∠DAB = ∠CBA = 90° ...(ii) [वर्ग का प्रत्येक कोण 90° है] [∵ ABCD एक वर्ग है।]
समीकरण (i) को समीकरण (ii) से घटाने पर, हम पाते हैं।
∠DAB – ∠OAB = ∠CBA – ∠OBA = 90° – 60°
यानी ∠DAO = ∠CBO = 30°
ΔAOD और ΔBOC में,
AO = BO ...[दिया गया है।] [समबाहु त्रिभुज की सभी भुजाएँ बराबर होती हैं।]
∠DAO = ∠CBO ...[ऊपर सिद्ध]
और AD = BC ...[एक वर्ग की भुजाएँ बराबर होती हैं।]
∴ ΔAOD ≅ ΔBOC ...[SAS सर्वांगसमता नियम द्वारा]
अत:, OD = OC ...[CPCT द्वारा]
ΔCOD में,
OC = OD
अत:, ΔCOD एक समद्विबाहु त्रिभुज है।
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
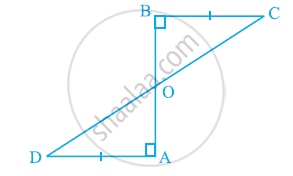
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिंदु है ताकि BD = `1/2` AC है। दर्शाइए कि ∠ABC एक समकोण है।
