Advertisements
Advertisements
Question
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
Solution
प्रश्न में दिया गया है, ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि A और D, BC के विपरीत भुजाओं पर स्थित हैं, AB = AC और DB = DC है।
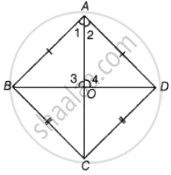
यह सिद्ध करने के लिए कि AD, BC का लम्ब समद्विभाजक है, अर्थात OB = OC है।
उपपत्ति - त्रिभुज BAD और त्रिभुज CAD में,
AB = AC ...[दिया गया है।]
BD = CD ...[दिया गया है।]
AD = AD ...[सामान्य पक्ष]
अब, सर्वांगसमता की SSS कसौटी से,
ΔBAD ≅ ΔCAD
इसलिए, ∠1 = ∠2 ...[CPCT]
अब, त्रिभुज BAO और त्रिभुज CAO में,
AB = AC ...[दिया गया है।]
∠1 = ∠2 ...[ऊपर सिद्ध]
AO = AO ...[सामान्य पक्ष]
इसलिए, सर्वांगसमता की SAS कसौटी से,
ΔBAO ≅ ΔCAO
चूंकि, BO = CO ...[CPCT]
और ∠3 = ∠4 ...[CPCT]
∠3 + ∠4 = 180° ...[रैखिक युग्म अभिगृहीत]
∠3 + ∠3 = 180°
2∠3 = 180°
∠3 = `(180^circ)/2`
∠3 = 90°
इसलिए, AD, BC के समद्विभाजक के लंबवत है।
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
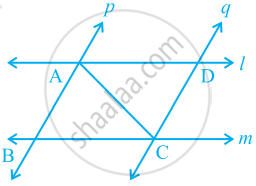
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
△ABC और △DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि:
- △ABD ≌ △ACD
- △ABP ≌ △ACP
- AP कोण A और कोण D दोनों को समद्विभाजित करता है।
- AP रेखाखंड BC का लम्ब समद्विभाजक है।
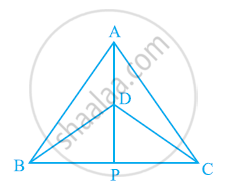
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
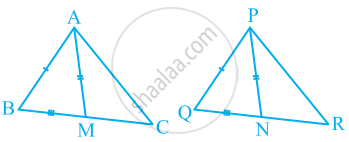
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
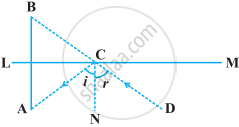
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
