Advertisements
Advertisements
Question
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
Solution
दिया गया है - ΔABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है।
साथ ही, AD और BE क्रमशः BC और AC भुजाओं पर दो शीर्षलंब हैं।
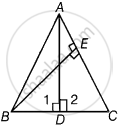
सिद्ध करना है - AE = BD
प्रमाण - ΔABC में,
AC = BC ...[दिया गया है।]
∠ABC = ∠CAB ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
अर्थात्, ∠ABD = ∠EAB ...(i)
ΔAEB और ΔBDA में,
∠AEB = ∠ADB = 90° ...[दिया गया है, AD ⊥ BC और BE ⊥ AC]
∠EAB = ∠ABD ...[समीकरण (i) से]
और AB = AB ...[उभयनिष्ठ भुजा]
∴ ΔAEB ≅ ΔBDA ...[AAS सर्वांगसमता नियम द्वारा]
⇒ AE = BD ...[CPCT द्वारा]
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
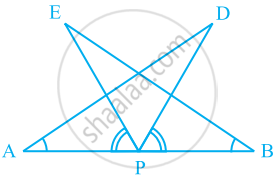
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
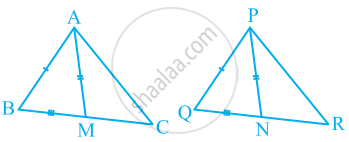
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
