Advertisements
Advertisements
Question
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
Solution
दिया गया है - ABCD एक चतुर्भुज है जिसमें AB = BC और AD = CD है।
दर्शाना है - BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
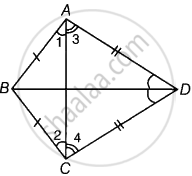
उपपत्ति - चूँकि, AB = BC ...(दिया गया है।)
∴ ∠2 = ∠1 ...(i) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
और AD = CD ...[दिया गया है।]
⇒ ∠4 = ∠3 ...(ii) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
समीकरण (i) और (ii) को जोड़ने पर, हम प्राप्त करते हैं।
∠2 + ∠4 = ∠1 + ∠3
⇒ ∠BCD = ∠BAD ...(iii)
ΔBAD तथा ΔBCD में,
AB = BC ...[दिया गया है।]
∠BAD = ∠BCD ...[समीकरण (iii) से]
और AD = CD ...[दिया गया है।]
∴ ΔBAD ≅ ΔBCD ...[SAS सर्वांगसमता नियम द्वारा]
अत:, ∠ABD = ∠CBD और ∠ADB = ∠CDB अर्थात, BD कोणों ABC और ADC को समद्विभाजित करता है। ...[CPCT द्वारा]
APPEARS IN
RELATED QUESTIONS
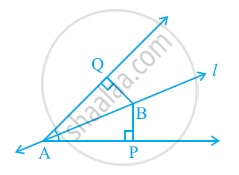
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
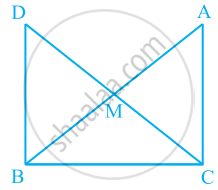
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
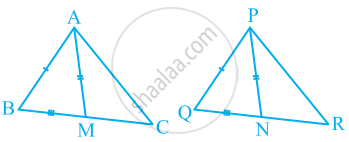
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
