Advertisements
Advertisements
Question
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
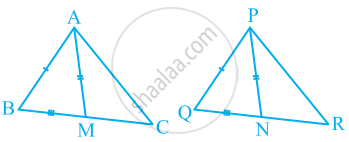
Solution
ΔABC में, AM, BC की माध्यिका है।
∴ BM = `1/2 BC`
ΔPQR में, PN, QR की माध्यिका है।
∴ QN = `1/2QR`
हालाँकि, BC = QR
∴ `1/2BC` = `1/2QR`
⇒ BM = QN …(1)
(i) ΔABM और ΔPQN में,
AB = PQ ...(दिया गया है)
BM = QN ...[समीकरण (1) से]
AM = PN ...(दिया गया है)
∴ ΔABM ≅ ΔPQN ...(SSS सर्वांगसमता नियम)
∠ABM = ∠PQN ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा)
∠ABC = ∠PQR …(2)
(ii) ΔABC और ΔPQR में,
AB = PQ ...(दिया गया है)
∠ABC = ∠PQR ...[समीकरण (2) से]
BC = QR ...(दिया गया है)
⇒ ΔABC ≅ ΔPQR ...(SAS सर्वांगसमता नियम से)
APPEARS IN
RELATED QUESTIONS
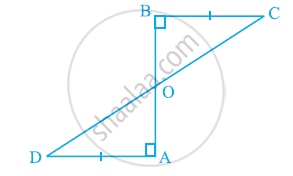
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
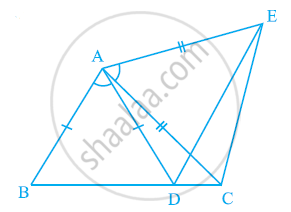
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
