Advertisements
Advertisements
प्रश्न
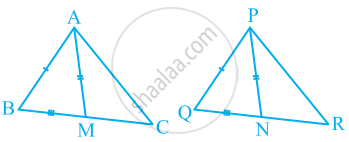
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
उत्तर
ΔABC में, AM, BC की माध्यिका है।
∴ BM = `1/2 BC`
ΔPQR में, PN, QR की माध्यिका है।
∴ QN = `1/2QR`
हालाँकि, BC = QR
∴ `1/2BC` = `1/2QR`
⇒ BM = QN …(1)
(i) ΔABM और ΔPQN में,
AB = PQ ...(दिया गया है)
BM = QN ...[समीकरण (1) से]
AM = PN ...(दिया गया है)
∴ ΔABM ≅ ΔPQN ...(SSS सर्वांगसमता नियम)
∠ABM = ∠PQN ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा)
∠ABC = ∠PQR …(2)
(ii) ΔABC और ΔPQR में,
AB = PQ ...(दिया गया है)
∠ABC = ∠PQR ...[समीकरण (2) से]
BC = QR ...(दिया गया है)
⇒ ΔABC ≅ ΔPQR ...(SAS सर्वांगसमता नियम से)
APPEARS IN
संबंधित प्रश्न
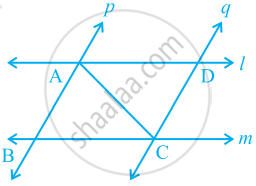
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
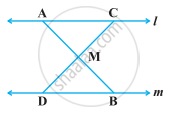
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है तथा ∠C का समद्विभाजक भुजा AB को D पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AC + AD = BC है।
