Advertisements
Advertisements
Question
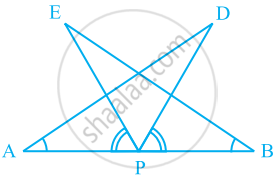
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
Advertisements
Solution
P, AB का मध्य-बिंदु है।
∴ AP =BP
∠EPA = ∠DPB ...[दिया गया है]
दोनों पक्षों में ∠EPD जोड़ने पर, हमें प्राप्त होता है:
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
i. अब, △DAP और △EBP में, हमारे पास है
∠PAD = ∠PBE ...[∵ ∠BAD = ∠ABE]
AP = BP ...[ऊपर सिद्ध किया गया है।]
∠DPA = ∠EPB ...[ऊपर सिद्ध किया गया है।]
∴ △DAP ≌ △EBP ...[ASA अनुरूपता द्वारा]
ii. चूँकि, △DAP ≌ △EBP
⇒ AD = BE ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
APPEARS IN
RELATED QUESTIONS
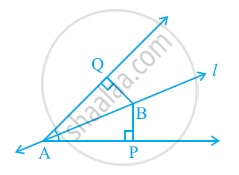
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
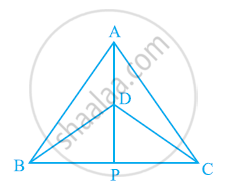
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
सिद्ध कीजिए कि एक समबाहु त्रिभुज को छोड़कर, किसी त्रिभुज में सबसे लंबी भुजा का सम्मुख कोण एक समकोण के `2/3` भाग से बड़ा होता हैं।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
