Advertisements
Advertisements
प्रश्न
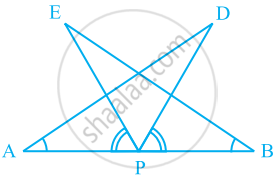
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
उत्तर
P, AB का मध्य-बिंदु है।
∴ AP =BP
∠EPA = ∠DPB ...[दिया गया है]
दोनों पक्षों में ∠EPD जोड़ने पर, हमें प्राप्त होता है:
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
i. अब, △DAP और △EBP में, हमारे पास है
∠PAD = ∠PBE ...[∵ ∠BAD = ∠ABE]
AP = BP ...[ऊपर सिद्ध किया गया है।]
∠DPA = ∠EPB ...[ऊपर सिद्ध किया गया है।]
∴ △DAP ≌ △EBP ...[ASA अनुरूपता द्वारा]
ii. चूँकि, △DAP ≌ △EBP
⇒ AD = BE ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
APPEARS IN
संबंधित प्रश्न
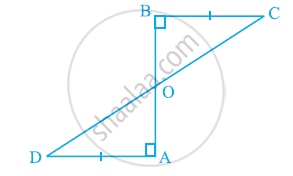
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
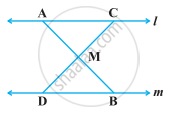
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है तथा ∠C का समद्विभाजक भुजा AB को D पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AC + AD = BC है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
