Advertisements
Advertisements
प्रश्न
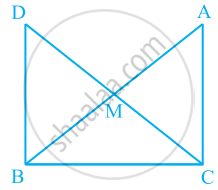
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
उत्तर
चूँकि M, AB का मध्य-बिंदु है।
∴ BM = AM
i. ΔAMC और ΔBMD में, हमारे पास है
CM = DM ...[दिया गया है]
∠AMC = ∠BMD ...[शीर्षाभिमुख कोण]
AM = BM ...[ऊपर सिद्ध किया गया है।]
∴ ΔAMC ≅ ΔBMD ...[SAS सर्वांगसमता से]
ii. चूँकि ΔAMC ≅ ΔBMD
∠MAC = ∠MBD ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
लेकिन वे एकांतर अंत: कोणों की जोड़ी बनाते हैं।
∴ AC ‖ DB
अब, BC एक तिर्यक रेखा है जो समांतर रेखाओं AC और DB को प्रतिच्छेद करती है।
∴ ∠BCA + ∠DBC = 180° ...[सह-अंत: कोण]
लेकिन ∠BCA = 90° ...[ΔABC, C पर समकोण है]
∴ 90° + ∠DBC = 180°
⇒ ∠DBC = 90°
iii. फिर से, ΔAMC ≅ ΔBMD ...[ऊपर सिद्ध किया गया है।]
∴ AC = BD ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
अब, ΔDBC और ΔACB में, हमारे पास है
BD = CA ...[ऊपर सिद्ध किया गया है।]
∠DBC = ∠ACB ...[प्रत्येक 90°]
BC = CB ...[उभयनिष्ठ]
∴ ΔDBC ≅ ΔACB ...[SAS सर्वांगसमता द्वारा]
iv. चूँकि, ΔDBC ≅ ΔACB
⇒ DC = AB ...[सर्वांगसम त्रिभुजों के संगत भागों द्वारा]
But DM = CM ...[दिया गया है]
∴ CM = `1/2` DC = `1/2` AB
⇒ CM = `1/2` AB
APPEARS IN
संबंधित प्रश्न
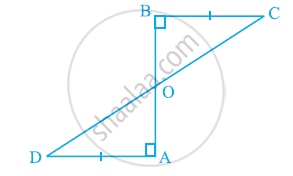
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
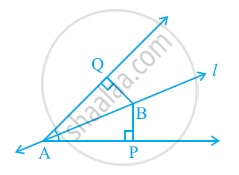
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
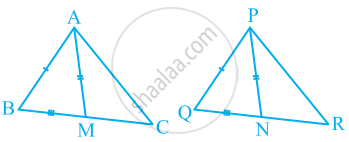
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है तथा ∠C का समद्विभाजक भुजा AB को D पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AC + AD = BC है।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
