Advertisements
Advertisements
Question
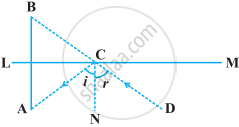
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
Solution 1
दिया गया है - एक बिंदु OA को बिंदु A पर रखा गया है, LM एक समतल दर्पण है, D एक प्रेक्षक है और OB प्रतिबिम्ब है।
सिद्ध करना है - प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी कि वस्तु दर्पण के सामने होती है अर्थात् OB = OA।

प्रमाण - CN ⊥ LM और AB ⊥ LM
⇒ AB || CN
∠A = ∠i [वैकल्पिक आंतरिक कोण] ...(i)
∠B = ∠r [संगत कोण] ...(ii)
साथ ही, ∠i = ∠r [∵ आपतन कोण = परावर्तित कोण] ...(iii)
समीकरण (i), (ii) और (iii) से,
∠A = ∠B
ΔCOB और ΔCOA में,
∠B = ∠A ...[ऊपर सिद्ध]
∠1 = ∠2 ...[प्रत्येक 90°]
और CO = CO ...[सामान्य पक्ष]
∴ ΔCOB ≅ ΔCOA ...[AAS सर्वांगसमता नियम द्वारा]
⇒ OB = OA ...[CPCT द्वारा]
अतः सिद्ध हुआ।
Solution 2
ΔOBC और ΔOAC में,
∠1 = ∠2 ...[प्रत्येक 90°]
साथ ही, ∠i = ∠r [∵ आपतन कोण = परावर्तन कोण] ...(i)
समीकरण के दोनों पक्षों (i) को –1 से गुणा करने पर और फिर दोनों पक्षों में 90° जोड़ने पर, हम प्राप्त करते हैं।
90° – ∠i = 90° – ∠r
⇒ ∠ACO = ∠BCO
और OC = OC ...[सामान्य पक्ष]
∴ ΔOBC ≅ ΔOAC ...[ASA सर्वांगसमता नियम द्वारा]
⇒ OB = OA ...[CPCT द्वारा]
अतः, प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी कि वस्तु दर्पण के सामने होती है।
APPEARS IN
RELATED QUESTIONS
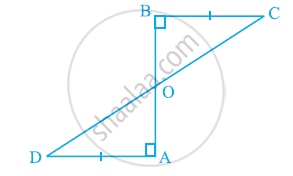
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
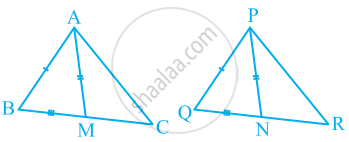
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 4 cm, 3 cm और 7 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
