Advertisements
Advertisements
Question
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
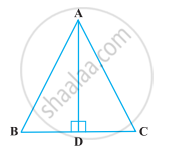
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
Solution
∆ABC में, AB = AC है।
⇒ ∠ACB = ∠ABC ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
∆ABD और ∆ACD में,
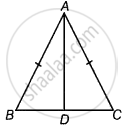
AB = AC ...[दिया गया है।]
∠ABD = ∠ACD ...[ऊपर सिद्ध]
∠ADB = ∠ADC ...[प्रत्येक 90°]
∴ ∆ABD ≅ ∆ACD ...[AAS द्वारा]
इसलिए, ∠BAD = ∠CAD ...[CPCT द्वारा]
इसलिए, दिए गए तर्क में दोष यह है कि पहले सिद्ध कीजिए कि ∠ABD = ∠ACD है।
अत:, ∠ABD = ∠ACD दोष है।
APPEARS IN
RELATED QUESTIONS
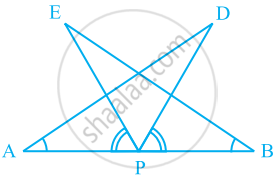
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
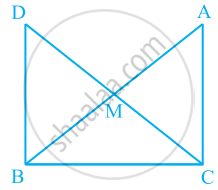
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
